Метод Черчмена Акоффа (последовательное сравнение)

Этот метод относится к числу наиболее популярных при оценке аль­тернатив. В нем предполагается последовательная корректиров­ка оценок, указанных экспертами. Основные предположения, на которых основан метод, состоят в следующем:

• каждой альтернативе 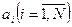ставится в соответствие действительное неотрицательное число j (a_i);

• если альтернатива a_i предпочтительнее альтернативы а_j, то j (a_i) > j (а_j), если же альтернативы a_i и а_j равноценны, то j (a_i) = j (а _j);

• если j (a_i) и j (а_j) оценки альтернатив a_i и а_j, то j (a_i) + j (а_j) соответствует совместному осуществлению альтернатив a_i и а_j. Наиболее сильным является последнее предположение об аддитивности оценок альтернатив.

Согласно методу Черчмена-Акоффа альтернативы а₁, а₂,..., a_N ранжируются по предпочтительности. Пусть для удобства из­ложения альтернатива а₁ наиболее предпочтительна, за ней сле­дует a₂ и т.д. Эксперт указывает предварительные численные оцен­ки j (а_i) для каждой из альтернатив. Иногда наиболее предпоч­тительной альтернативе приписывается оценка 1, остальные оценки располагаются между 0 и 1 в соответствии с их предпоч­тительностью. Затем эксперт производит сравнение альтернати­вы a₁ и суммы альтернатив а ₂,..., a_N. Если а₁ предпочтительнее, то эксперт корректирует оценки так, чтобы

В противном случае должно выполняться неравенство

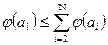
Если альтернатива а_i оказывается менее предпочтительной, то для уточнения оценок она сравнивается по предпочтению с суммой альтернатив а₂,а₃,..., a_N-1 и т.д. После того как альтернатива а_i оказывается предпочтительнее суммы альтернатив а₂,..., a_k(k³2), она исключается из рассмотрения, а вместо оцен­ки альтернативы a₁ рассматривается и корректируется оценка аль­тернативы а _2. Процесс продолжается до тех пор, пока откоррек­тированными не окажутся оценки всех альтернатив.

При достаточно большом N применение метода Черчмена-Акоффа становится слишком трудоемким. В этом случае целесо­образно разбить альтернативы на группы, а одну из альтерна­тив, например максимальную, включить во все группы. Это по­зволяет получить численные оценки всех альтернатив с помощью оценивания внутри каждой группы.

Метод Черчмена-Акоффа является одним самых эффектив­ных. Его можно успешно использовать при измерениях в шкале отношений. В этом случае определяется наиболее предпочтитель­ная альтернатива а_i1. Ей присваивается максимальная оценка. Для всех остальных альтернатив эксперт указывает, во сколько раз они менее предпочтительны, чем а_i1. Для корректировки числен­ных оценок альтернатив можно использовать как стандартную процедуру метода Черчмена-Акоффа, так и попарное сравнение предпочтительности альтернатив. Если численные оценки аль­тернатив не совпадают с представлением эксперта об их пред­почтительности, производится корректировка.

Дата добавления: 2014-01-07