Второй закон термодинамики

Второй закон термодинамики. Энтропия. Вычисление изменения энтропии для различных процессов. Постулат Планка. Энергия Гиббса и энергия Гельмгольца. Уравнение Гиббса-Гельмгольца. Самопроизвольное протекание химических реакций. Расчет изменения энергии Гиббса в химических реакциях. Химический потенциал. Активность и летучесть.

Первый закон термодинамики не дает критериев направления самопроизвольных и несамопроизвольных процессов и условий, при которых наступает состояние равновесия. Лишь с появлением в термодинамике понятия энтропия появляется строгий критерий направления самопроизвольных процессов. Термин энтропия, как и второй закон термодинамики, были введены Клаузиусом в середине ХIХ века. Карно показал, что в тепловых машинахтеплота, полученная от источника тепла, не может быть полностью переведена в механическую работу, а часть ее должна быть передана третьему телу – холодильнику. Это обобщение по существу выражает второй закон термодинамики и может рассматриваться как одна из формулировок второго закона термодинамики. Рассмотрим также некоторые другие формулировки второго закона:

Формулировка Клаузиуса (1850 г.). Не возможен самопроизвольный процесс передачи теплоты от холодного тела к горячему.

Формулировка Кельвина (Томсона) (1851 г .). Не возможно превратить теплоту какого-либо тела в работу, не производя никакого другого действия, кроме охлаждения этого тела;

Формулировка по Оствальду. Вечный двигатель второго рода невозможен (т.е. не существует машины, которая бы полностью превращала теплоту в работу).

Клаузиус, рассматривая обратимый циклический процесс, состоящий из двух изотерм и двух адиабат (см. учебники), разбил его на бесконечно малые участки, просуммировал (учитывая знаки dQ) все величины 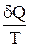(элементарная приведенная теплота), и показал, что для обратимого процесса

.

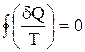Если вспомнить свойства функции состояния, то для какой-то функции состояния Z интеграл 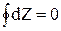, поэтому величина 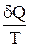связана с какой-то функцией состояния. Эту функцию состояния назвали энтропией (S).

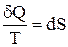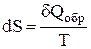или , (1)

Выражение 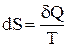(равенство Клаузиуса) – это дифференциальная форма записи второго закона термодинамики для обратимых процессов. Для необратимых процессов, как показал Клаузиус, справедливо неравенство

dS > 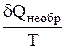, (2)

это дифференциальная форма записи второго закона термодинамики для необратимых процессов. В общем виде дифференциальная форма записи второго закона термодинамики для обратимых и необратимых процессов может быть представлена в виде:

dS 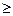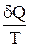, (3)

Единица измерения энтропии - такая же как и у соответствующей теплоемкости: молярной (мольной) – , удельной – .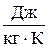

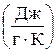Энтропия – экстенсивная величина, т.е. пропорциональна массе системы.

Из дифференциальной формы записи второго закона термодинамики легко можно получить интегральную форму записи этого закона:

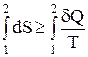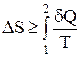; (4)

Первый и второй законы термодинамики можно объединить в так называемый объединенный первый и второй закон термодинамики, который для обратимых процессов можно записать следующим образом:

ТdS = dU + dA¢ + pdV. (5)

Если работа производится системой только против внешнего давления, то dA¢ = 0 и получаем:

ТdS = dU + pdV (6)

Отсюда вытекает, что:

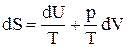, (7)

т.е. энтропия S является функцией внутренней энергии U и объема V: S = f(U,V).

В общем виде объединенный первый и второй закон термодинамики можно записать следующим образом:

ТdS 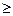dU + dA¢ + pdV (8)

Если рассматривать только объемную работу, то получим:

TdS 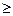dU + pdV (9)

Второй закон термодинамики для изолированных систем.

Для изолированной системы dQ = 0, m = const, U = const, V = const. Для необратимых процессов, протекающих в такой системе, можно записать, что

dS_необр. > 0

DS_необр. > 0 т.е. S₂ > S₁ (11)

Выражения dS > 0 и DS > 0 можно рассматривать как математическую запись второго закона термодинамики, который для изолированной системы формулируется следующим образом:

в изолированной системе любой самопроизвольный процесс протекает только с увеличением энтропии, причем процесс закончится тогда, когда энтропия S достигнет своего максимального значения (когда наступит состояние равновесия).

При равновесии S₂ = S_max = const и DS = 0. Схематически все сказанное можно изобразить на графике зависимости S от пути процесса:

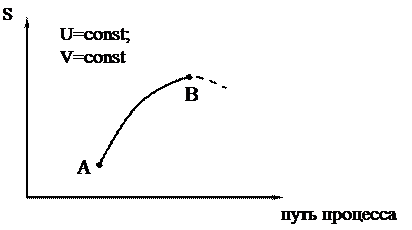Путь процесса – это какая-либо величина, которая меняется при протекании процесса и поддается опытному определению.

Участок АВ – необратимый самопроизвольный процесс (DS > 0), энтропия возрастает; участок ВA – необратимый нeсамопроизвольный процесс (DS < 0), энтропия уменьшается; точка В – равновесное состояние (S=S_max).

Следует отметить, что если процесс протекает в неизолированной системе, то для оценки необратимости процесса необходимо иметь величину изменения энтропии системы и величину изменения энтропии окружающей среды.

Дата добавления: 2014-01-07