Элементы теории деформаций

Характерной чертой движения сплошной среды является ее деформация, т. е. изменение расстояния между отдельными точками среды.

Можно доказать, что удлинение (или укорочение) произвольно направленного единичного отрезка , проходящего через какую-либо точку М(х₁, х₂, х₃) среды, вычисляется по формуле

(1.16)

где α _i =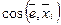— направляющие косинусы отрезка; ε_ii — удлинения (укорочения) единичных отрезков, направленных параллельно координатным осям ox_i; ε_ij = ε_ji(i≠j) — изменения первоначально прямых углов, образованных отрезками, направленными параллельно координатным осям ox_i и ох_j.

Таким образом, деформация элементарного объема среды в окрестности точки М полностью определяется шестью величинами ε_ij, которые называются компонентами симметричного тензора деформаций.

Для малых (по сравнению с единицей) деформаций верны следующие соотношения Коши:

в декартовой системе координат

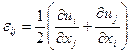(i,j=1, 2, 3), (1.17)

где u_i — компоненты вектора перемещения в точке М.

В цилиндрической системе координат (r, Θ, z) при осевой симметрии

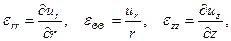
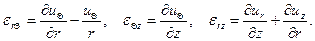(1.18)

Компоненты вектора перемещений u_r, u_Θ, u_z связаны с компонентами u _i (i = 1, 2, 3) обычными соотношениями преобразования координат при повороте системы вокруг оси oz:

u_r= u₁cos Θ + u₂sin Θ,

u_Θ= - u₁ sin Θ + u₂cos Θ, u_z= u₃.

Если иметь в виду связь между координатами x₁ = r cos Θ, x₂ = r sin Θ и x₃ = z, то доказать справедливость перехода от формул (1.17) к формулам (1.18), или наоборот, не представляет труда.

Так как деформация отрезка не зависит от выбора направлений координатных осей, то правая часть в формуле (1.16) инвариантна преобразованию системы координат, т. е.

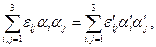(1.19)

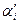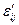где и — направляющие косинусы и компоненты деформаций в новой 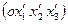системе координат. Для вычисления 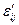через ε_ij, достаточно в равенстве (1.19) выразить 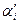через α_i и сравнить коэффициенты при одинаковых α_i, α_j.

В любой точке тела всегда существует по крайней мере одна тройка взаимно перпендикулярных направлений, таких, что деформация элемента в окрестности точки определяется только удлинением (укорочением) ε_ii = ε_i вдоль этих направлений без изменения прямых углов (ε_ij = 0, i≠j). Такие направления называются главными осями деформаций, а величины ε_i (i = 1, 2, 3) — главными удлинениями, которые могут быть найдены из следующего кубического уравнения:

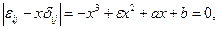
где 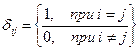— символ Кронекера. Ясно, что коэффициенты этого уравнения не зависят от выбора системы координат, т. е. они инвариантны. Первый коэффициент ε этого уравнения

(1.20)

и имеет простой геометрический смысл — относительное изменение объема в окрестности точки. Коэффициенты а и b геометрического смысла не имеют и поэтому не являются характеристикой деформаций.

Характеристикой искажения формы элемента сплошной среды служит инвариантная величина

Г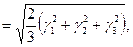

называемая интенсивностью деформаций сдвига. Величины γ₁ = ε₂ - ε₃, γ₂ = ε₃ – ε₁, γ₃ = ε₁ – ε₂ называются главными сдвигами.

Известно приближенное соотношение

Г=1,08γ_mах,

где γ_mах — наибольший из главных сдвигов.

В произвольной декартовой системе координат величина Г вычисляется по формуле

Г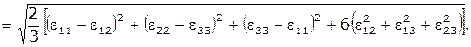 (1.21)

Иногда пользуются величиной ε _u = 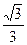Г, называемой приведенной деформацией или интенсивностью деформаций.

Для характеристики деформационного состояния служит параметр Надаи

(1.22)

который изменяется в пределах от -1 (при чистом удлинении) до +1 (при частичном укорочении). В случае чистого сдвига μ_ε = 0. При всестороннем расширении (или сжатии) μ_ε смысла не имеет.

Часто удобно пользоваться следующим представлением компонент деформаций:

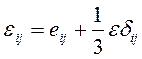, (1.23)

где e_ij —компоненты, характеризующие только деформации сдвига, называемые компонентами девиатора деформаций, δ_ij —символ Кронекера. Отсюда следует, что компоненты тензора деформации растяжения (сжатия) ε_ii отличаются от соответствующих компонент девиатора е_ii на 1/3 объемной деформации, а компоненты деформации сдвига не отличаются, т. е.

Если известны компоненты деформации ε_ij как функции декартовых координат х_i, то для однозначного определения 3-х компонент u_i вектора перемещений из 6-ти соотношений (1.17) необходимо и достаточно, чтобы функции ε_ij удовлетворяли условиям совместимости (или неразрывности) деформаций Сен-Венана:

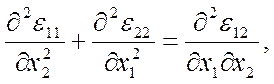
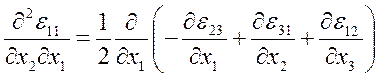(1.24)

и т. д., всего 6 условий (остальные получаются из выписанных круговой заменой индексов 1→2→3→1).

Таким образом, условия совместимости (1.24) являются уравнениями, которые связывают компоненты ε_ij тензора деформаций.

Для анализа больших деформаций, если главные оси при деформации не поворачиваются, используются так называемые натуральные удлинения (укорочения)

где l_i0, l_i —начальные и текущие длины элемента в соответствующих направлениях.

Характерные соотношения для малых деформаций являются справедливыми и для натуральных удлинений.

Дата добавления: 2014-01-07