Рационал функцияларды интегралдау

Рационал функцияларды интегралдау мәселесі бізді дұрыс рационал бөлшекті интегралдауға әкеледі. Дұрыс рационал бөлшекті интегралдау үшін оны жәй бөлшектер қосындысына жіктеп алып, содан кейін интегралдаймыз.

Мысалдар. Рационал бөлшектерді интегралдаңыз.

1. .

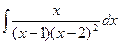Шешуі. Дұрыс рационал бөлшекті жәй бөлшектердің қосындысына жіктеп жазамыз:

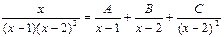, мұндағы А, В және С коэффициенттері табылуға тиісті белгісіз коэффициенттер. Ол үшін теңдіктің оң жағын ортақ бөлімге келтіріп, қосындысын табамыз:

.

Соңғы теңдіктегі бөлшектердің бөлімдері тең болғандықтан, алымдарын теңестіріп, ықшамдап жазып аламыз:

немесе

.

Бұл теңдіктегі 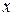- тің бірдей дәрежелерінің коэффициенттерін теңестіріп, теңдеулер жүйесін аламыз:

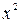
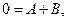
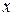
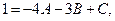
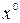
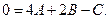
Теңдеулер жүйесінен A =1; B =-1; C =2.

Сонда бастапқы бөлшекті мына түрде жазуға болады:

.

Енді интегралды есептейміз:

.

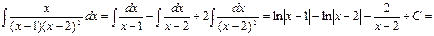
2. .

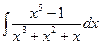Шешуі. Берілген бөлшек бұрыс рационал бөлшек. Сондықтан көпмүшені көпмүшеге бөлу тәсілімен оның бүтін бөлігін бөліп алып,

,

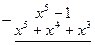
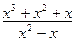
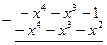
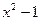бұрыс бөлшекті оның бүтін бөлігі мен дұрыс бөлшектің қосындысы түрінде жазамыз: . Сонда

.

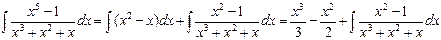Үшінші қосылғышта интеграл астындағы дұрыс бөлшектің бөлімін көбейткіштерге жіктейміз: 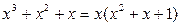. Дұрыс рационал бөлшекті жәй бөлшектердің қосындысына жіктеп жазамыз: 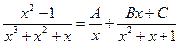, мұндағы А, В және С белгісіз коэффициенттер. Теңдіктің оң жағын ортақ бөлімге келтіріп, қосындысын табамыз:

.

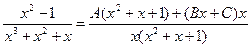Соңғы теңдіктегі бөлшектердің алымдарын теңестіріп, ықшамдап жазып аламыз:

.

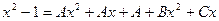Бұл теңдіктегі 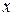- тің бірдей дәрежелерінің коэффициенттерін теңестіріп, теңдеулер жүйесін аламыз:

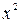
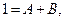
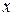
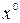
Теңдеулер жүйесінен: A =-1; 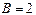; С =1.

Сонда бөлшек мына түрде жазылады:

.

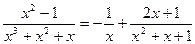Енді интегралды есептейміз:

.

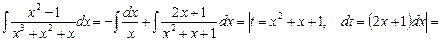
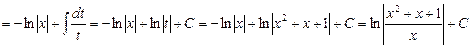Бастапқы интегралға оралып, есептің жауабын аламыз:

.

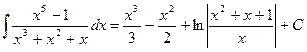Тұжырымдалған теореманың негізінде дұрыс рационал бөлшекті интегралдау, төмендегідей төрт жәй бөлшектерді интегралдауға әкеледі:

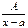I. ; II. ; III. ;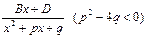

IV. 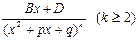, мұнда - нақты сандар.

І және ІІ түрдегі жәй бөлшектерді интегралдау кестелік интегралдарға келтіріледі:

І. .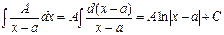

II. .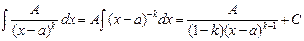

III. түрдегі интегралды есептеу үшін интеграл астындағы бөлшекті алымындағы бөлшек бөлімінің туындысы болып табылатын 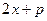қосылғышы бөлек бөлініп шығатындай етіп түрлендіреміз.

Тригонометриялық өрнектерді интегралдау

1. түріндегі 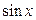және функцияларынан тәуелді рационал функцияның интегралы.

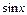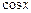Бұл түрде берілген интегралды есептеу үшін және функцияларын арқылы өрнектеп, ауыстыруын қолданып, интеграл астындағы өрнекті рационал бөлшекке келтіреміз, яғни мына формулаларды қолданамыз:

, ,

.

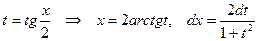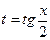- ауыстыруын әмбебап ауыстыру формуласы деп атайды.

Әмбебап ауыстыруды қолданғаннан кейін, берілген интеграл 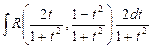рационал функцияның интегралы түрінде жазылады.

Көптеген жағдайларда тригонометриялық функцияның қасиеттерін ескеріп, басқа ауыстыруларды қолдану, бұл түрдегі интегралды есептеуді жеңілдетеді. Дербес жағдайларда ұтымды болатын тригонометриялық функцияларды интегралдау әдістерін қарастырайық.

а) Егер 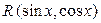функциясы 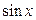функциясына қатысты тақ болса, яғни теңдігі орындалса, онда 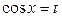ауыстыруын қолданамыз.

б) Егер 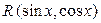функциясы 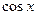функциясына қатысты тақ болса, яғни теңдігі орындалса, онда ауыстыруын қолданамыз.

в) Егер 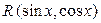функциясы 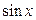және функциялары бойынша жұп болса, яғни 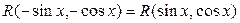теңдігі орындалса, онда ауыстыруын қолданамыз.

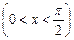2. бүтін нақты сандар түріндегі интегралдар.

а) Егер – жұп оң сандар болса, онда төмендегі формулаларды:

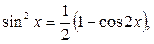
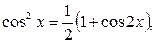
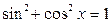
қолданып, интеграл астындағы функцияның дәрежесін төмендетіп, интегралдаймыз.

б) Егер – сандарының екеуі де тақ және ең болмағанда біреуі теріс болса, онда немесе 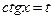ауыстыруларын қолданамыз.

в) Егер - бүтін оң тақ сан болса, онда ауыстыруын, ал егер - бүтін оң тақ сан болса, онда 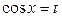ауыстыруын қолданамыз.

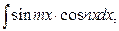
3. түріндегі интегралдар.

Мына формулаларды:

,

,

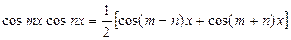
қолданып, интегралдарды қосылғыштарға жіктеп алып, интегралдаймыз.

1.

.

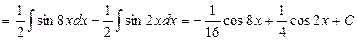2.

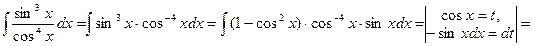
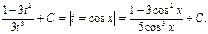
6-дәріс. Риман интеграл

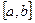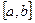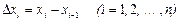функциясы аралығында үзіліссіз болсын. аралығын нүктелерімен бөлікке бөлейік. деп әр бөліктің ұзындығын белгілейік. Әрбір бөлікшеден қалауымызша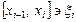 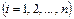бір нүктеден алып, 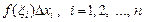көбейтінділері арқылы қосынды құрайық:

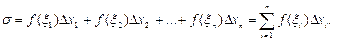(12)

(12) қосынды 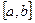аралығынан алынған интегралдық қосынды деп аталады.

Анықтама. Егер , (12) интегралдық қосынды 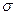, 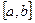аралығын бөлу тәсілінен және нүктелерін таңдап алуымыздан тәуелсіз, (12) теңдіктің шегі бар және шектеулі болса, онда ол шек аралығындағы Риманша алынған 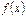функциясының анықталған интегралы немесе Риман интегралы деп аталады және оны былай белгілейді:

Сонымен, анықтама бойынша

мұндағы 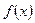- интеграл астындағы функция, - интеграл астындағы өрнек, а саны - интегралдың төменгі шегі, b саны - интегралдың жоғарғы шегі, ал х айнымалысы - интегралдау айнымалысы деп аталады.

Теорема. 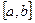аралығында үзіліссіз 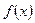функциясының сол аралықта анықталған интегралы бар болады.

Анықталған интегралдың қасиеттері

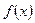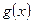және функциялары 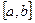аралығында Риман бойынша интегралданатын болсын.

1⁰. Егер интегралдың жоғарғы шегі мен төменгі шегінің орындарын ауыстырсақ, онда оның таңбасы өзгереді:

.

2⁰. Анықталған интегралдың жоғарғы шегі мен төменгі шегі өзара тең болса, онда ол нөлге тең: .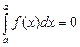

3⁰. Егер және функциялары 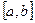аралығында интегралданатын болса, онда 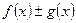да осы аралықта интегралданатын болады және

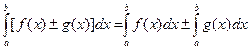
теңдігі орындалады.

4⁰. Егер функциясы аралығында интегралданатын болса, онда 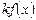көбейтіндісі де (мұнда 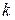- тұрақты сан) осы аралықта интегралданатын болады және

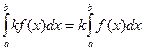
теңдігі орындалады.

5⁰. Егер 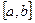аралығын 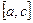және 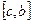аралықтарына бөлсек, онда

.

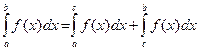6⁰. Егер 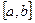аралығындағы х айнымалысының барлық мәндері үшін 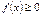болса, онда

.

7⁰. Егер 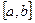аралығындағы х айнымалысының барлық мәндері үшін 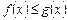болса, онда

.

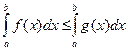8⁰. Егер 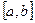аралығында 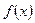функциясының ең үлкен және ең кіші мәндері сәйкес M және m сандары болса, онда

Дата добавления: 2014-01-07