
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Штік интегралда айнымалыларды алмастыру формуласы
|
|
|
|
.
.
Немесе  ретімен де интегралдауға болады:
ретімен де интегралдауға болады:
Міне, осылай ретін алмастырсақ, жалпы алты рет алмастырып есептеуге болады, яғни үш еселі интегралдың мәні ретін ауыстырудан тәуелсіз болатындығын көреміз.
б)  тектес денеде интегралдау.
тектес денеде интегралдау.
 |
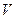 облысының
облысының 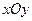 жазықтығына түсірілген проекциясы
жазықтығына түсірілген проекциясы 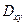 болсын,
болсын, 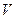 облысының үстінгі және астыңғы шекаралары
облысының үстінгі және астыңғы шекаралары  және
және
 болсын, интегралдық қосындыны тапқанда х, у - тердің өзгермеуін қамтамасыз етіп,
болсын, интегралдық қосындыны тапқанда х, у - тердің өзгермеуін қамтамасыз етіп,  бойынша қосып алғаннан кейін жазықтықтағы облыс
бойынша қосып алғаннан кейін жазықтықтағы облыс 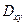 бойынша қосамыз, сонда келесідей болады:
бойынша қосамыз, сонда келесідей болады:

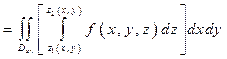
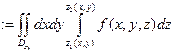 ,
,
мұндағы,  .
.
Егер 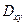 облысы
облысы  осіне қарағанда дұрыс облыс болса, яғни
осіне қарағанда дұрыс облыс болса, яғни 
 онда
онда
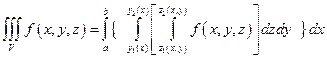 .
.
Мысалы,  интегралын есептеңіз, мұндағы
интегралын есептеңіз, мұндағы  жазықтығы және координаталар жазықтықтарымен шенелген облыс.
жазықтығы және координаталар жазықтықтарымен шенелген облыс.
Шешуі. 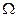 - ның
- ның 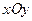 жазықтығына түсірілген проекциясы
жазықтығына түсірілген проекциясы 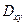 :
: ,
,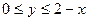 болады, ал
болады, ал 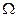 - ның үстіңгі және астыңғы беттері сәйкесінше
- ның үстіңгі және астыңғы беттері сәйкесінше  және
және 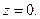 Сонда
Сонда
 .
.
15-дәріс. Еселі интегралдар
Полярлық координаталар жүйесінде қос интегралды есептеу
Егер шектелген тұйық  облысының шекара сызығын полярлық координаталар жүйесіндегі теңдеуімен жазу ыңғайлы болса, сонымен қатар интегралданатын
облысының шекара сызығын полярлық координаталар жүйесіндегі теңдеуімен жазу ыңғайлы болса, сонымен қатар интегралданатын 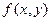 функциясы да полярлық координатамен жеңіл жазылса, онда полярлық координаталар жүйесінде қос интегралды есептеу мәселесін қарастырамыз.
функциясы да полярлық координатамен жеңіл жазылса, онда полярлық координаталар жүйесінде қос интегралды есептеу мәселесін қарастырамыз.
Егер 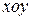 жазықтығындағы
жазықтығындағы  облысының әрбір нүктесі
облысының әрбір нүктесі  жазықтығындағы
жазықтығындағы  облысының сәйкес нүктесіне (және керісінше)
облысының сәйкес нүктесіне (және керісінше)
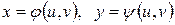
өрнектері арқылы сәйкес бейнеленсе, онда қос интегралдағы айнымалыларды ауыстыру формуласы былай жазылады:
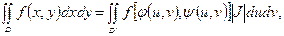
мұндағы
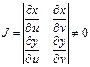
Якобиан немесе Якоби анықтауышы деп аталады. Полярлық координаталарға көшу формуласы

Полярлық координаталар жүйесінің полярлық нүктесі мен полярлық өсі тік бұрышты координаталар жүйісінің бас нүктесімен 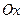 өсінің оң жарты өсімен сәйкестікте болғанда, келесідей координаталар алмастыруларын енгіземіз:
өсінің оң жарты өсімен сәйкестікте болғанда, келесідей координаталар алмастыруларын енгіземіз:
 ,
,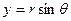 .
.
Сонда интегралданатын функция  , ал аудан элементі
, ал аудан элементі 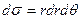 болады, яғни
болады, яғни
 .
.
Жоғарыдағы өрнектің оң жағындағы қос интегралды есептеу мәселесі екі еселі интегралды есептеуге келтіріледі. Полярлық координаталар жүйесіндегі интегралдау облыстары үшін қос интегралды есептеудің үш түрлі жағдайын қарастырамыз.
Бірінші жағдай. Полярлық нүкте интегралдау облысы  - ның сыртында болсын.
- ның сыртында болсын.

Онда  облысын
облысын 



 ,
,



 теңсіздіктері арқылы жазамыз. Сонда полярлық координаталар жүйесіндегі қос интеграл төмендегідей екі еселі интегралға айналады:
теңсіздіктері арқылы жазамыз. Сонда полярлық координаталар жүйесіндегі қос интеграл төмендегідей екі еселі интегралға айналады:
 .
.
Екінші жағдай. Полярлық нүкте интегралдау облысы  - ның шекарасында болсын.
- ның шекарасында болсын.
 |
Онда  облысын
облысын 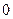



 ,
,



 теңсіздіктері арқылы жазамыз. Сонда полярлық координаталар жүйесіндегі қос интеграл төмендегідей екі еселі интегралға айналады:
теңсіздіктері арқылы жазамыз. Сонда полярлық координаталар жүйесіндегі қос интеграл төмендегідей екі еселі интегралға айналады:
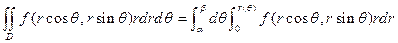 .
.
Үшінші жағдай. Полярлық нүкте интегралдау облысы  - ның ішінде болсын.
- ның ішінде болсын.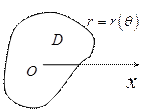
Онда  облысы
облысы  қисығымен қоршалады да полярлық нүкте
қисығымен қоршалады да полярлық нүкте  - ның ішкі бөлігінде болады, әрі оны
- ның ішкі бөлігінде болады, әрі оны 



 ,
,



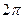 теңсіздіктері арқылы жазамыз. Сонда полярлық координаталар жүйесіндегі қос интеграл төмендегідей екі еселі интегралға айналады:
теңсіздіктері арқылы жазамыз. Сонда полярлық координаталар жүйесіндегі қос интеграл төмендегідей екі еселі интегралға айналады:
 .
.
Ескерту. Жоғарыда айтылған 
 және
және  теңдеулерінің барлығы қисықтың полярлық координаталар жүйесіндегі теңдеулері болғандықтан, интегралдау облысы
теңдеулерінің барлығы қисықтың полярлық координаталар жүйесіндегі теңдеулері болғандықтан, интегралдау облысы  - ның шекарасы тік бұрышты координаталар жүйесіндегі теңдеулерімен берілген кезде, алдымен қисықтың теңдеуін полярлық координата теңдеуіне (теңдеудегі х, у - терді сәйкесінше
- ның шекарасы тік бұрышты координаталар жүйесіндегі теңдеулерімен берілген кезде, алдымен қисықтың теңдеуін полярлық координата теңдеуіне (теңдеудегі х, у - терді сәйкесінше 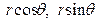 - ларға ауыстырып ықшамдасақ болғаны) айналдырып, содан кейін есептеуге сай келетін формуламен қос интегралды есептейміз.
- ларға ауыстырып ықшамдасақ болғаны) айналдырып, содан кейін есептеуге сай келетін формуламен қос интегралды есептейміз.
Мысалы, 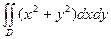 қос интегралын есептеңіз. Мұндағы, интегралдау облысы
қос интегралын есептеңіз. Мұндағы, интегралдау облысы  сақина тәрізді облыстың бір бөлігі, яғни,
сақина тәрізді облыстың бір бөлігі, яғни, 



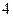 ,
, 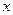
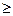
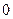 ,
, 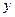
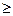
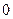 .
.
Шешуі.Интегралдау облысы  суретте көрсетілген түрде болады.
суретте көрсетілген түрде болады.
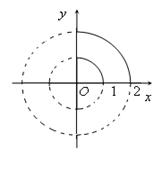 |
Интегралдау облысы  тікбұрышты координаталар жүйесіндегі 7.9-суретте көрсетілгендей
тікбұрышты координаталар жүйесіндегі 7.9-суретте көрсетілгендей 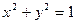 және
және 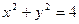 дөңгелек теңдеулері, олар полярлық координаталар жүйесінде сәйкесінше
дөңгелек теңдеулері, олар полярлық координаталар жүйесінде сәйкесінше 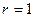 және
және 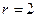 болады. Сонда полярлық координаталар жүйесінде интегралдау облысы
болады. Сонда полярлық координаталар жүйесінде интегралдау облысы  келесі түрде жазылады:
келесі түрде жазылады:




 ,
,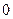



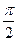 .
.
Олай болса формула бойынша

 .
.
Үштік интегралды есептеуде айнымалыларынан жаңа
айнымалыларынан жаңа 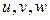 айнымалыларына көшу
айнымалыларына көшу 
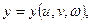
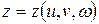 функциялары арқылы өрнектелсін. Бұл
функциялары арқылы өрнектелсін. Бұл 

 функциялары бірінші дербес туындыларымен бірге үзіліссіз болып,
функциялары бірінші дербес туындыларымен бірге үзіліссіз болып,  жазықтығының
жазықтығының  облысының әрбір нүктесін,
облысының әрбір нүктесін,  жазықтығының
жазықтығының 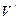 облысының әрбір нүктесіне өзара бір мәнді бейнелесе, үштік интегралдағы айнымалыны ауыстыру келесі түрде жазылады:
облысының әрбір нүктесіне өзара бір мәнді бейнелесе, үштік интегралдағы айнымалыны ауыстыру келесі түрде жазылады:
 ,
,
мұндағы,  анықтауышы якобиан деп аталады.
анықтауышы якобиан деп аталады.
Аталған алмастыруымызды келесідей айтуға да болады:
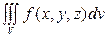 үштік интегралына төмендегідей ауыстырулар жасалық:
үштік интегралына төмендегідей ауыстырулар жасалық:
 ,
,  ,
,
әрі бұл алмастыруымыз оң болсын деп жориық, онда ол келесі шарттарды қанағаттандыруы керек:
1) 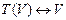 арасында бір мәнді сәйкестік бар;
арасында бір мәнді сәйкестік бар;
2)  функцияларының
функцияларының  - да
- да  - лар бойынша үзіліссіз дербес туындылары бар болады, әрі оған кері болатын
- лар бойынша үзіліссіз дербес туындылары бар болады, әрі оған кері болатын  бейнелеуі
бейнелеуі  - да
- да  - тер бойынша үзіліссіз дербес туындылары бар болады;
- тер бойынша үзіліссіз дербес туындылары бар болады;
3) 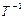 түрлендіруінің якобианы
түрлендіруінің якобианы
 болады, ал ол
болады, ал ол  - да нөльден өзгеше болады, сондықтан келесі теңдік орындалады:
- да нөльден өзгеше болады, сондықтан келесі теңдік орындалады:
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2260; Нарушение авторских прав?; Мы поможем в написании вашей работы!