Дебиеттер тізімі

.

5. Декарттық координаталардан цилиндрлік және сфералық кординаталарға көшу формулалары

а) Цилиндрлік координаталар

Цилиндрлік координаталар жүйесі деп 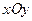жазықтығындағы полярлық координаталар жүйесіне 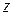өсі қосып жасалынған жүйені айтады, Цилиндрлік координаталар жүйесіндегі көлем элементі 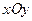жазықтығындағы аудан элементі 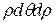мен 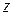өсіндегі биіктік элементі 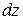- тің көбейтіндісі, яғни 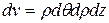болады. Ендеше цилиндрлік координаталар жүйесінде координаталарды алмастыру формуласы

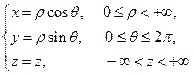
болғандықтан, Якобиан мына түрде болады:

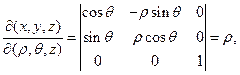
үштік интегралдағы цилиндрлік координаталарға көшу формуласы:

,

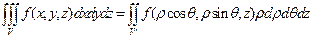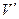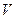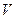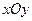мұндағы дегеніміз - ның цилиндрлік алмастырудан кейінгі бейнесі. Цилиндрлік координаталарды пайдаланып үштік интегралдарды есептегенде, үнемі - ның жазықтығына түсірілген проекциялық облыс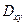- ты табу керек болады. Яғни,

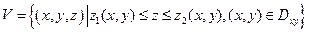болғанда, цилиндрлік координаталар үшін формула мына түрде болады:

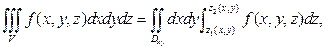
мұндағы, қос интеграл бөлігін полярлық координаталар жүйесінде есептейміз.

Мысалы, 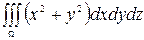интегралын есептеңіз, мұндағы 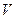: 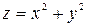және 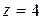беттерімен қоршалған кеңістік.

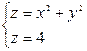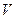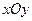Екі теңдеуді біріктіріп шешсек, яғни , онда -ның жазықтығына түсірілген проекциялық облысы 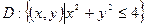табылады.

облысында 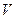- ның үстіңгі жағы 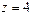, ал астыңғы жағы 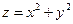болады, полярлық координатаны пайдалансақ, D: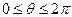, , 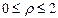ал 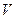- ның үстіңгі жағы 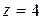, ал астыңғы жағы 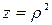болады. Сондықтан

=.

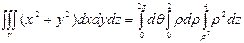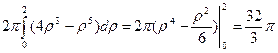б) Сфералық координаталар

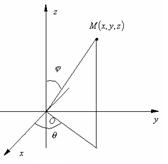
Сфералық координаталар жүйесінде, кеңістіктегі кез келген бір 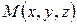нүктесін келесідей айтуға болады: осы нүктеден координаталар

бас нүктесіне дейінгі ара қашықтық 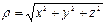, 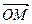векторы мен 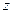өсінің оң бағыты арасындағы сүйір бұрыш 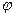, ал 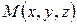нүктесінің 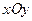жазықтығына түсірілген проекциясы 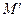пен бас нүктеден жасалған 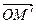векторы арасындағы бұрыш болсын, сондықтан кеңістіктегі кез келген бір нүкте 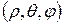реттелген сандар тобына сәйкес келеді, міне бұл 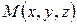нүктесінің сфералық координатасы болады.

M’

Сфералық координаталар жүйесінде координаталарды алмастыру формуласы келесідей болады:

,

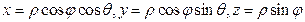әрі 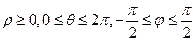, , 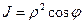көлем элементі .

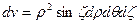Бұл алмастыру көбінесе интегралданатын функция 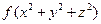типті болғанда қолданылады. Сонда үштік интегралдағы сфералық координаталарға көшу формуласы келесідей болады:

,

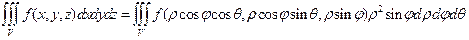м ұндағы 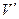дегеніміз 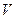- ның сфералық алмастырудан кейінгі бейнесі.

Сфералық координаталар жүйесінде, 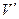облысы:

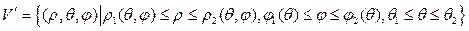
жиынымен анықталғанда, жоғарыдағы сфералық координаталарға көшу формуласы келесідей болады:

=.

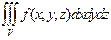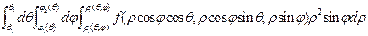Мысалы, 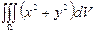интегралын есептеңіз, мұндағы 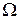: 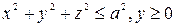оң жарты сферасымен қоршалған облыс.

Сфералық координаталар жүйесінде интегралдау облысы

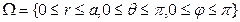болады, сондықтан

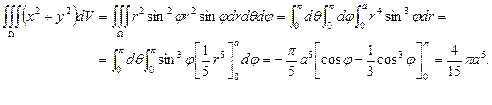
Қос интегралдың қолданылулары

1. Қос интеграл арқылы жазық фигураның ауданын есептеу

Берілген облысы арқылы шектелген жазық фигураның ауданы келесі формуламен есептелінеді:

.

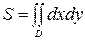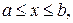
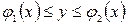Егер облысы арқылы анықталса, онда

.

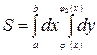Егер облысы полярлық координаталар жүйесінде 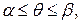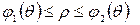теңсіздіктерімен анықталса, онда

.

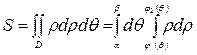2. Қос интеграл арқылы дене көлемін есептеу.

үстіңгі жағынан үзіліссіз 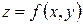бетімен, астыңғы жағынан облысымен, бүйір жағынан жасаушысы 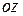өсіне параллель, ал бағыттаушысы облысының контуры болып келген цилиндрлік дене көлемі келесі формуламен есептелінеді:

.

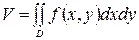3. Қос интегралдың механикада қолданылуы.

Егер Оху жазықтығының облысымен шектелген пластинаның массасы М келесі қос интеграл арқылы есептеледі:

.

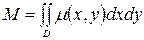Мұндағы 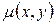пластина тығыздығы.

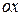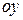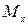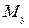Пластинаның және остеріне қарағандағы статикалық моменттері және келесі формуламен есептелінеді:

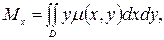
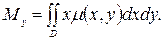
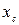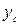Пластинаның ауырлық центрінің координаталары және келесі формуламен есептелінеді:

.

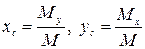Ал инерция моменттері келесі формуламен есептелінеді:

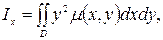
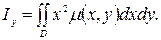
Пластинаның бас нүктеге қарағандағы инерция моменті:

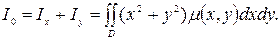
Негізгі әдебиеттер.

1. Я.С. Бугров, С.М. Никольский Дифференциальное и интегральное исчисление. т.1,2. М.: Наука, 1985г.

2. В.А. Ильин, Э.Т. Позняк. Основы мат. анализа. т.1,2. М.: Наука, 1971, 1980.

3. Н.С.Пискунов Дифференциальное и интегральное исчисление для втузов. т.1,2. М.: Наука, 1985г.

4. Г. Н.Берман. Сборник задач и упражнений по мат. анализу. М.– 1985.

Қосымша әдебиеттер

5. С.Б.Әубәкір. Жоғары математика. 1-2 бөлімдер Алматы, ҚазҰТУ. 2001

6. Е.Ж.Айдос Жоғары математика. Алматы. «Ильтех-Кітап» ЖШС, 2003 ж.

7. С.М.Никольский. Курс математического анализа. т.1,2. М.: Наука, 1983.

8. Г.М.Фихтенгольц. Курс дифференциального и интегрального исчисления. т.1-3. М.: Наука,1969.

9. А. П.Рябушко и др. Индивидуальные задания по высшей математике. т.1-3. Минск: «Вышэйшая школа», 2002.

10. В.Ф.Бутузов и др. Математический анализ в вопросах и задачах. Уч.пособие для вузов. М.– Высшая школа.– 1984.

Дата добавления: 2014-01-07