Понятие метрического пространства

Основные функциональные пространства

Лекция 5

ТЕМА 2.

Одной из важнейших операций анализа является предельный переход. В основе этой операции лежит тот факт, что на числовой прямой определено расстояние от одной точки до другой. Многие фундаментальные факты анализа не связаны с алгебраической природой действительных чисел (т. е. с тем, что они образуют поле), а опираются лишь на понятие расстояния. Обобщая представление о действительных числах как о множестве, в котором введено расстояние между элементами, мы приходим к понятию метрического пространства — одному из важнейших понятий современной математики.

Определение.

Метрическим пространством называется пара (X, ρ), состоящая из некоторого множества (пространства) X элементов (точек) и расстояния, т. е. однозначной, неотрицательной, действительной функции ρ(х,у), определенной для любых x и y из X и подчиненной следующим аксиомам;

1. ρ(х,у) ≥ 0 для всех х,у,

2. ρ(х,у) = 0 тогда и только тогда, когда х=у,

3. ρ(х,у) = ρ(y,x) (аксиома симметрии),

4. ρ(х,z) £ ρ(х,у) + ρ(у,z) (аксиома треугольника).

Само метрическое пространство, т. е. пару (X, ρ), мы будем обозначать, как правило, одной буквой R = (X, ρ).

В случаях, когда недоразумения исключены, мы будем зачастую обозначать метрическое пространство тем же символом, что и сам «запас точек» X.

Приведем примеры метрических пространств. Некоторые из этих пространств играют в анализе весьма важную роль.

Примеры.

1. Положив для элементов произвольного множества

мы получим, очевидно, метрическое пространство. Его можно назвать пространством изолированных точек.

2. Множество действительных чисел с расстоянием

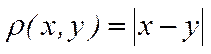образует метрическое пространство R¹.

3. Множество упорядоченных групп из n действительных чисел x = (х₁, …, x_n) с расстоянием

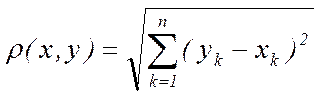(1)

называется n -мерным арифметическим евклидовым пространством Rⁿ. Справедливость аксиом 1) - 3) для Rⁿ очевидна. Покажем, что в Rⁿ выполнена и аксиома треугольника.

Пусть x = (x₁,…, x_n), y = (y₁,…, y_n),

z = (z₁,…, z_n);

тогда аксиома треугольника записывается в виде

(2)

Полагая , получаем 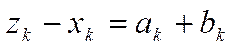, а неравенство (2) принимает при этом вид

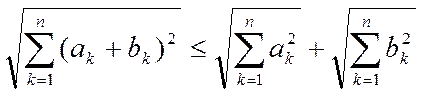(3)

Но это неравенство сразу следует из известного неравенства Коши—Буняковского[1]

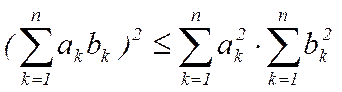(4)

Действительно, в силу этого неравенства имеем

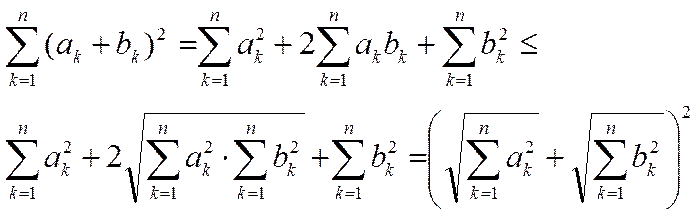тем самым неравенство (3), а следовательно и (2), доказано.

4. Рассмотрим то же самое множество упорядоченных групп из n действительных чисел x = (x₁,…, x_n) но расстояние определим в нем формулой

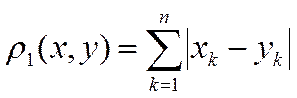. (5)

Справедливость аксиом здесь очевидна.

Задача. Доказать аксиому 4.

Обозначим это метрическое пространство символом .

5. Возьмем снова то же самое множество, что и в примерах 3 и 4, и определим расстояние между его элементами формулой

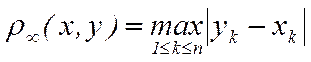. (6)

Справедливость аксиом 1) — 3) очевидна.

Задача. Доказать аксиому 4.

Это пространство, которое мы обозначим 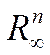, во многих вопросах анализа не менее удобно, чем евклидово пространство Rⁿ.

Последние три примера показывают, что иногда и в самом деле важно иметь различные обозначения для самого метрического пространства и для множества его точек, так как один и тот же запас точек может быть по-разному метризован.

6. Множество C[a,b] всех непрерывных действительных функций, определенных на сегменте [a, b], с расстоянием

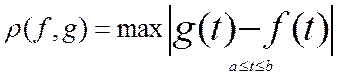(7)

также образует метрическое пространство. Аксиомы 1) — 3) проверяются непосредственно.

Задача. Доказать аксиому 4.

Это пространство играет очень важную роль в анализе. Мы будем его обозначать тем же символом C[a, b], что и само множество точек этого пространства. Вместо C[0,1] мы будем писать просто С.

7. Обозначим через l₂ метрическое пространство, точками которого служат всевозможные последовательности х=(x₁,…,х_n, …) действительных чисел, удовлетворяющие условию ,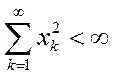

а расстояние определяется формулой

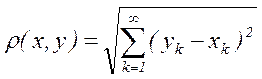. (8)

Из элементарного неравенства следует, что функция ρ(х,у) имеет смысл для всех 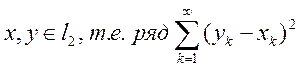сходится, если

/

Покажем теперь, что функция (8) удовлетворяет аксиомам метрического пространства. Аксиомы 1) - 3) очевидны, а аксиома треугольника принимает здесь вид

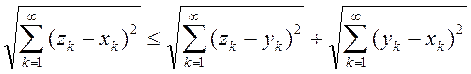
В силу сказанного выше каждый из трех написанных здесь рядов сходится. С другой стороны, при каждом n справедливо неравенство

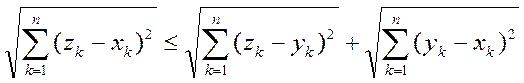(9)

(см. пример 4). Переходя здесь к пределу при n®∞ получаем (8), т.е. неравенство треугольника в l₂.

8. Рассмотрим, как и в примере 6, совокупность всех функций, непрерывных на отрезке [a, b], но расстояние определим иначе, а именно, положим

. (10)

Такое метрическое пространство мы будем обозначать С₂[a, b] и называть пространством непрерывных функций с квадратичной метрикой. Здесь все аксиомы метрического пространства очевидны, а аксиома треугольника непосредственно вытекает из интегральной формы неравенства Коши — Буняковского[2]

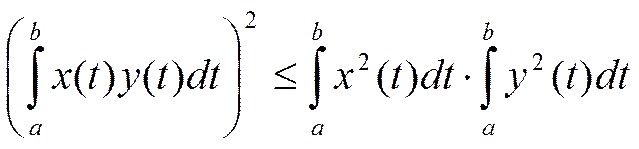
9. Рассмотрим множество всех ограниченных последовательностей x = (x₁,…, x_n, …) действительных чисел.

Положив

, (11)

мы получим метрическое пространство, которое обозначим m. Справедливость аксиом очевидна.

10. Множество упорядоченных групп из n действительных чисел с расстоянием

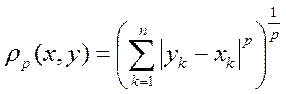, (12)

где р — любое фиксированное число ≥ 1, представляет собой метрическое пространство, которое мы обозначим .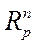

Проверим аксиому 4.

Пусть x=(x₁,…,x_n), y=(y₁,…,y_n), z=(z₁,…,z_n).

Положим 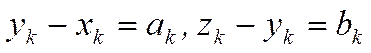, тогда неравенство

справедливость которого мы должны установить, примет вид

(13)

Это — так называемое неравенство Минковского. При p= 1 неравенство Минковского очевидно (модуль суммы не превосходит суммы модулей), поэтому будем считать, что р > 1.

Доказательство неравенства (13) при р>1 основано на так называемом неравенстве Гёльдера

(14)

где числа р > 1 и q > 1 связаны условием

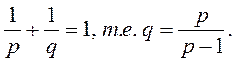(15)

Заметим, что неравенство (14) однородно. Это значит, что если оно выполнено для каких-либо двух векторов a = (a₁,…, a_n), и b = (b₁,…, b_n), то оно выполнено и для векторов λa и μb, где λ и μ — произвольные числа. Поэтому неравенство (14) достаточно доказать для случая, когда

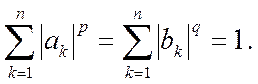(16)

Итак, пусть выполнено условие (16); докажем, что

(17)

Рассмотрим на плоскости (ξ,η) кривую, определяемую уравнением η = ξ^p-1 (ξ>0), или, что то же самое, уравнением ξ^p-1 (η >0) (рис. 1). Из рисунка ясно, что при любом выборе положительных значений a и b будет S₁ + S₂ > ab. Вычислим площади S₁ и S₂:

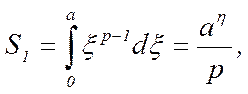
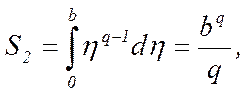
Таким образом, справедливо числовое неравенство

Заменив здесь a на |a_k| и b на |b_k| и суммируя по k от 1 до n, получим, учитывая (15) и (16),

Неравенство (17), а, следовательно, и общее неравенство (14) доказаны.

При р = 2 неравенство Гёльдера (14) переходит в неравенство Коши — Буняковского (4).

Перейдем теперь к доказательству неравенства Минковского. Для этого рассмотрим тождество

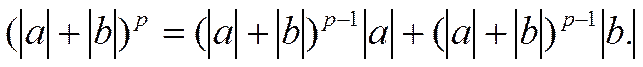
Заменяя в написанном тождестве a на a_k и b на b_k и суммируя по k от 1 до n получим

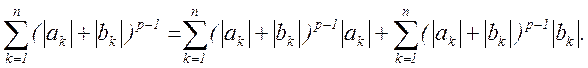
Применяя теперь к каждой из двух сумм, стоящих справа, неравенство Гёльдера и учитывая, что (p - 1)q = p, получим

Делим обе части этого неравенства на

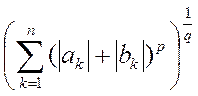
получим

откуда сразу следует неравенство (13). Тем самым установлена аксиома треугольника в пространстве .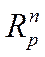

Рассмотренная в этом примере метрика ρ_р превращается в евклидову метрику (пример 3) при р = 2 и в метрику примера 4 при р = 1. Можно показать, что метрика

,

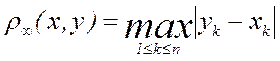введенная в примере 5, является предельным случаем метрики ρ_р (х, у), именно:

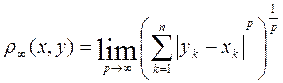
Из неравенства

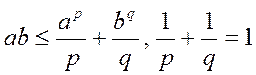
установленного выше, легко выводится и интегральное неравенство Гёльдера

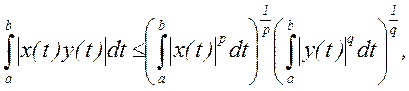
справедливое для любых функций x(t) и y(t), для которых стоящие справа интегралы имеют смысл. Отсюда в свою очередь получается интегральное неравенство Минковского

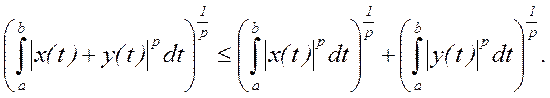
11. Укажем еще один интересный пример метрического пространства. Его элементами являются всевозможные последовательности действительных чисел x = (x₁, …,x_n, …), такие, что

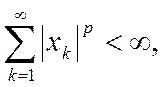
где р ≥ 1 — некоторое фиксированное число, а расстояние определяется формулой

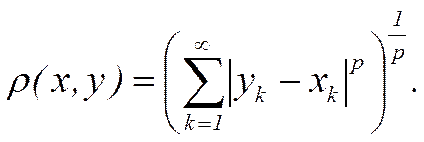(18)

Это метрическое пространство мы обозначим l_p.

В силу неравенства Минковского (13) имеем при любом n

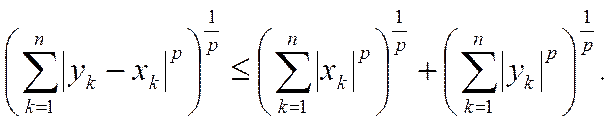
Так как, по предположению, ряды

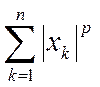и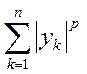

сходятся, то, переходя к пределу при n ® ∞, получим

(19)

Таким образом, доказано, что формула (18), определяющая расстояние в l_p, действительно имеет смысл для любых 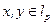. Одновременно неравенство (19) показывает, что в l_p выполнена аксиома треугольника. Остальные аксиомы очевидны.

Неограниченное количество дальнейших примеров дает следующий прием. Пусть R = (X, ρ) — метрическое пространство и M — любое подмножество в X. Тогда М с той же функцией ρ(х,у), которую мы считаем теперь определенной для x и у из М, тоже представляет собой метрическое пространство; оно называется подпространством пространства R.

Дата добавления: 2014-01-07