Пряма в просторі

Под принципами управления следует понимать руководящие правила, основные положения и нормы поведения, которыми руководствуются органы управления в силу социально-экономических условий, сложившихся в обществе.

Принципы

Закономерности

Закон пропорциональности и композиции

Формулировка закона: «Каждая материальная система стремится сохранить в своей структуре все необходимые элементы (композицию), находящиеся в заданном подчинении (пропорции)».

Закон реализуется за счёт использования следующих принципов:

1. Принцип планирования: «Каждая организация должна иметь обоснованный план деятельности и развития».

2. Принцип координации: «Каждая организация должна следить за стратегическими, текущими и оперативными изменениями и вносить соответствующие коррективы в механизм выполнения».

3. Принцип полноты: «Каждая организация должна выполнять весь набор функций производства и управления на своём участке деятельности либо своими силами, либо с помощью привлечённых организаций».

Первая закономерность: единство системы управления производством. Единство системы управления означает устойчивость внутренних связей системы при изменении состояния внешней среды.

Вторая закономерность: пропорциональность производства и управления. Предусматривает оптимальное сочетание управляющей (администрации) и управляемой (производство) подсистем.

Третья закономерность: централизация и децентрализация управления. Оптимальное сочетание централизации и децентрализации управления означает необходимость распределения задач, функций и полномочий (прав и ответственности по уровням иерархии управления).

Четвёртая закономерность: соотносительность и адекватность управляющей и управляемой систем. Под соотносительностью следует понимать соответствие управляющей системы управляемой. В результате воздействия многочисленных факторов внешней и внутренней среды эти подсистемы постоянно меняются. При этом очень важно для сохранения управляемости соблюдение адекватности управляющей подсистемы управляемой.

1. Принцип духовной ориентации управления. Заключается в том, что менеджмент в процессе адаптации к постоянно меняющимся условиям и объектам управления опирается на национальную философию и не выходит за рамки духовных ценностных ориентиров народа и государства.

2. Принцип демократического централизма. В его основу положено сочетание централизованного руководства хозяйством и самостоятельности его отдельных элементов.

3. Принцип единства политического и хозяйственного руководства. Определяет соподчинённость целей общества, реализуемых определёнными политическими системами и целей хозяйствующих субъектов, функционирующих в рамках этих политических систем.

4. Принцип планового ведения хозяйства. Означает установление на длительный период направления, темпов и пропорций развития производства.

5. Принцип материального и морального стимулирования. Поскольку удовлетворение потребностей каждого человека и коллектива соответствует количеству и качеству затраченного труда, в управлении широко используют материальное и моральное стимулирование.

6. Принцип научности управления. Соблюдение принципа научности управления заключается в построении всей системы управления производством на новейших данных науки управления.

7. Принцип ответственности. Использование принципа ответственности означает: создание чёткой организационной структуры; тщательную разработку положений о подразделениях организации, должностных инструкций для исполнителей; установление точно определённой материальной ответственности хозрасчётных подразделений за упущения в работе; разработку положений о премировании и депремировании работников; чёткое оформление приказов и распоряжений и проведение других организационных мероприятий.

8. Принцип правильного подбора и расстановки кадров. Данный принцип означает, что подбор и расстановка кадров должны производится так, чтобы каждый на вверенном ему участке мог наиболее эффективно выполнять порученную работу.

9. Принцип экономичности и эффективности. В производстве необходимо добиваться не только эффективного сочетания людских и материальных ресурсов, но и наибольшей экономии сил и наиболее производительного применения труда. Этот принцип управления предполагает наиболее эффективное решение производственных задач. Соблюдение этого принципа ведёт к повышению конкурентоспособности продукции.

10. Принцип оптимального сочетания отраслевого и территориального управления. Реализация этого принципа должна способствовать специализации и комплексному развитию хозяйства регионов.

11. Принцип преемственности хозяйственных решений. В основе этого принципа лежит единство экономических явлений и процессов как последовательности количественных и качественных изменений, осуществляемых во времени и в пространстве. Этот принцип находит многообразные формы проявления. Преемственность хозяйственных решений необходима при разработке и особенно реализации плана с тем, чтобы информация сохраняла сопоставимость, Преемственность необходима при организационных решениях, оптимальность которых предполагает анализ прошлого, максимальное сохранение положительного опыта.

1) Пряма в просторі l – це перетин двох площин П₁ і П₂:

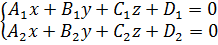— загальні рівняння прямої l у просторі.

2) Рівняння прямої через точку М₀(х₀,y₀,z₀) і напрямний (паралельний) вектор ` t = (m,n,p). (` t¹ `0). Виводиться як на площині:

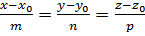; ці ж рівняння називають також канонічними рівняннями прямої в просторі.

Позначимо це відношення через t, t – параметр, t Î(-∞;∞), отримаємо

параметричні рівняння прямої:

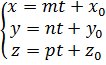, t Î ℝ.

3) Рівняння прямої через дві точки.

Точка M(x,y,z) лежить на прямій M₁M₂ (M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂)) тоді і тільки тоді, коли вектори 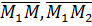колінеарні:

.

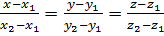Кут між прямими це кут між відповідними напрямними векторами. Для гострого кута: cos α=.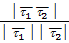

Кут між прямою і площиною. Нехай задані рівняння прямої і площини:

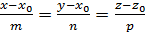, Ax+By+Cz+D =0. Позначимо через β кут між напрямним вектором прямої` t = (m,n,p) і нормальним вектором площини `N=(A, B, C), а кут між прямою і площиною через α. Тоді .

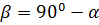Ми можемо знайти cos β, а cosβ =cos(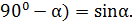

Отже, для гострого кута α маємо:

sin α=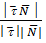. (Тому, що sin(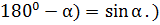

Розглянемо деякі задачі з рівняннями площини та прямої у просторі.

1) Перехід від загальних рівнянь прямої до канонічних.

` t `N₂

`N₁

Пряма в просторі l – це перетин двох площин П₁ і П₂: 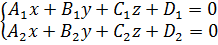Це загальні рівняння прямої.

Для того щоб скласти канонічні рівняння прямої, потрібно знайти напрямний вектор прямої` t і координати одної точки на прямій.

`N<sub>1</sub>=(A<sub>1</sub>,B<sub>1</sub>,C<sub>1</sub>),`N₂= (A₂,B₂,C₂) - нормальні вектори до площин. Напрямний вектор до прямої` t є перпендикулярним до векторів`N₁,`N<sub>2</sub>, отже,` t паралельний до векторного добутку`N<sub>1</sub> ´`N₂.

Для того щоб знайти точку на прямій, можна одній невідомій надати конкретного значення (наприклад, z=0), отримаємо систему рівнянь 2´2 для знаходження інших координат точки.

Приклад. Перейти від загальних рівнянь прямої до канонічних. .

`N<sub>1</sub>=(1,3,-1),`N₂=(2,1,-3) – перпендикулярні вектори до напрямного вектора` t.

` t = `N₁ ´`N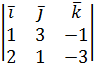<sub>2</sub>= =` i (-9+1) -` j (-3+2) +` k (1-6) = (-8;1;-5).

Нехай z =5, то система прийме вигляд: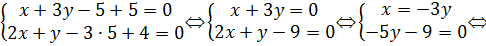

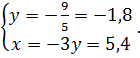
Отже, точка М(5,4; -1,8; 5) лежить на прямій. Тоді

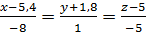– канонічні рівняння прямої.

2) Перетин прямої та площини

Перетин прямої та площини це точка (або Æ). ЇЇ зручно шукати, якщо пряма задана параметричними рівняннями, а площина загальним рівнянням.

Нехай задана пряма l: 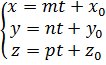, t Î ℝ і площина П: Ax+By+Cz=0.

Щоб знайти їх перетин потрібно об’єднати всі рівняння і розв’язати систему. Зручно в рівняння площини підставити х,у,z з рівнянь прямої через параметр t.

Отримаємо одне рівняння з одною невідомою t (лінійне). Знайшовши t підставимо його в параметричні рівняння прямої, щоб отримати координати точки перетину.

Приклад. Знайти точку перетину прямої та площини: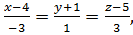

4x-3y+z-3=0.

Перейдемо до параметричних рівнянь прямої: 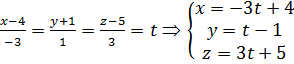. Підставимо в рівняння площини:

4(-3t+4)-3(t-1)+3t+5-3=0 Þ -12t+21=0 Þ t=21/12=7/4=1,75. Підставимо в параметричні рівняння: x= -1,25; y=0,75; z=10,25.

Перевірка: Точка з такими координатами належить прямій, бо вона отримана з параметричних рівнянь при деякому значенні t, тому потрібно підставити точку тільки в рівняння площини: 4×(-1,25)-3×0,75+10,25-3=0 Û 0=0.

Відповідь: М(-1,25; 0,75; 10,25).

Дата добавления: 2014-01-07