Лекція 15,16. Дійсні числа

План:

1. Поняття ірраціонального додатного числа.

2. Дійсні числа, дії над ними.

3. Від‘ємні числа.

1.Поняття ірраціонального додатного числа.

Дії над раціональними числами зручно виконувати, коли вони записані десятковими дробами. Тому краще і результати вимірів величин представляти в виді десяткових дробів. Якщо уявити процес десяткового виміру довжини відрізку в ідеалі(як це роблять в математиці), то можливі два варіанта: 1) на якомусь кроці процес виміру відрізку скінчиться. Тоді довжина відрізку 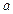буде виражена скінченим десятковим дробом виду 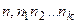. 2) описаний процес виміру довжини відрізку нескінчений. Тоді його представляють символом 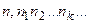, який називають нескінченим періодичним дробом. Існують відрізки, довжина яких не являються періодичним десятковим дробом, тобто раціональним числом, при вибраній одиниці виміру. Такі нескінчені неперіодичні десяткові дроби називають додатними ірраціональними числами. Ірраціональні числа можна отримати і при знаходженні радикалів із деяких раціональних чисел, наприклад , а також ірраціональними є чис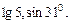ла числа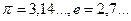

Множину додатних ірраціональних чисел позначають .

2. Дії над дійсними числами.

Множина додатних дійсних чисел - це об‘єднання множини додатних раціональних чисел і множини додатних ірраціональних чисел. Тому будь-яке дійсне число можна представити в виді нескінченого десяткового дробу – періодичного, якщо воно раціональне, або неперіодичного, якщо воно ірраціональне.

Дії над додатними раціональними числами зводяться, в принципі, до дій над натуральними числами.

Дії над нескінченими десятковими дробами можна звести до дій над раціональними, але необхідно ввести поняття приблизного значення дійсного числа за нестачею і залишком.

Число має приблизним значенням за нестачею з точністю до 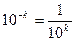таке число(тобто це число отримаємо, якщо залишимо цілу частину числа , і перші к цифр після коми). Приблизним значенням числа з залишком з точністю до 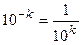називають число 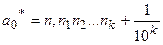(тобто це число отримаємо, якщо в запису 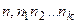останню цифру збільшити на 1).

Сумою дійсних чисел називається число 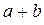, яке задовольняє нерівності .

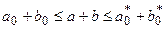Наприклад, знайти суму двох чисел з точністю до 0,001. Розглянемо їх приблизні значення 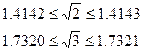, отже 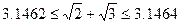і з точністю до 0,001 маємо .

Добутком дійсних чисел 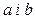називається число 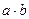, яке задовольняє нерівності .

Наприклад, обчислити добуток чисел 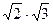з точністю до 0,1. Отримаємо 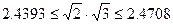,значить, з точністю 0.1 маємо .

Закони додавання і добутку дійсних чисел:

2) комутативний 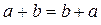і

3) асоціативний і

4) дистрибутивний .

3. Від’ємні числа.

На координатній вісі усі точки, що стоять праворуч нуля являються додатними, а числа, що стоять ліворуч нуля називаються від’ємними. Числа, наприклад, 1 і -1 називають протилежними. Число нуль не являється ні додатним ні від’ємним. Усі точки координатної вісі відповідні дійсним числам. Множина дійсних чисел і координатна вісь знаходяться у взаємно однозначній відповідності: кожному дійсному числу відповідає єдина точка координатної прямої і навпаки. Відстань від нуля до точки, координата якої є число , називається модулем числа. Записують так 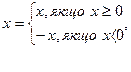. Наприклад, .

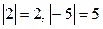Дії над числами:

1. Порівняння дійсних чисел: число 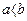, якщо воно розташовано лівіше на координатній прямій. Наприклад, 148>-2489, 214<6500.

2. Сумою двох дійсних чисел називається число 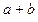, що задовольняє умовам:

1). Сума додатних чисел є число додатне; наприклад, 123+56=179

2). Сума від’ємних чисел є число від’ємне: додаємо модулі доданків і в переді ставимо знак мінус; наприклад, -12+(-45)=-57.

3). Сума чисел з різними знаками - це число, яке має знак такий, як і доданок з більшим модулем, а модуль суми – це різниця між доданками з більшим і меншим модулем, наприклад, 96+(-54)=42, -56+48=-8.

3. Добутком чисел є число 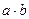, яке задовольняє умовам:

1). Добуток додатних чисел є число додатне, наприклад,

2). Добуток від’ємних чисел є число додатне; наприклад,

3). Добуток чисел з різними знаками є число від’ємне, наприклад, .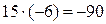

4. Віднімання і ділення – це дії, обернені додаванню і множенню.

Дата добавления: 2014-01-07