Методы определения порядка реакции

На практике исследование скорости химических реакций начинают с определения порядков этой реакции по каждому из реагирующих веществ и (или) порядка реакции в целом. Для реакции с участием нескольких веществ определить можно только поэтапно, определяя порядки по отдельным веществам. Для этого используется метод избытка (метод изоляции, метод Оствальда), а затем определяют n_i любым из описанных ниже методов.

Метод изоляции или метод избытка.

Если в исследуемой реакции участвуют несколько реагирующих веществ, то общий порядок реакции , где n_i - порядок по каждому из участников. Частный порядок n_i можно определить, взяв все вещества, кроме данного, взять в большом избытке. Так, в случае реакции

А + В + С ® D

скорость равна

.

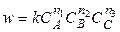Если вещества В и С взяты в большом избытке, то при протекании реакции их концентрации практически не изменяются, т.е.

.

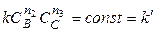И

.

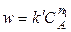Тогда, определив порядки реакции по каждому из реагирующих веществ, можно найти общий порядок реакции:

n = n ₁ + n ₂ + n ₃.

Метод подстановки.

Этот метод заключается в том, что опытные результаты - текущие концентрации веществ в моменты времени t - последовательно подставляются в интегральные кинетические уравнения реакций нулевого (7), первого (9), второго (12 или 14) порядков и определяется, какое из уравнений дает практически постоянную величину константы скорости. Именно это уравнение и определяет порядок исследуемой реакции.

Графический вариант метода подстановки.

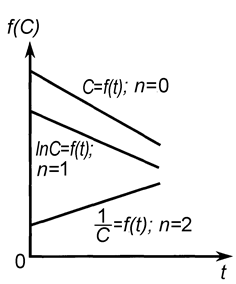
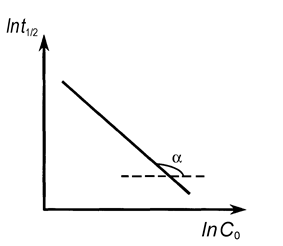
Рис. 9. Линейные зависимости различных функций концентрации реагирующих веществ от времени.

Рис. 10. Определение порядка реакции по зависимости времени полупревращения от начальной концентрации

Графический метод состоит в построении зависимостей различных функций концентрации от времени и определения, для какой из них наблюдается прямолинейная зависимость.

Линейные зависимости для реакций различных порядков получаются в следующих координатах (рис. 9): нулевого порядка С = f (t), первого порядка ln С = f (t), второго порядка 1/ С = f (t).

Для реакций более высоких порядков выбираются координаты 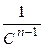- t.

Метод определения порядка реакции по времени полупревращения.

Порядок реакции определяется на основе опытной зависимости времен полупревращения (t _1/2) от начальных концентраций веществ (C ₀).

Как уже отмечалось, для n = 0 время полупревращения прямо пропорционально величине С₀, для n = 1 - не зависит от С₀, а n = 2 - обратно пропорционально С₀. Для реакции любого другого порядка справедливо соотношение (20)

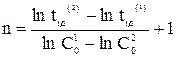, (20)

где t _1/2⁽¹⁾ и t _1/2⁽²⁾ - время полупревращения при начальных концентрациях С ₀₁ и С ₀₂, соответственно.

Возможен графический вариант метода: по оси ординат откладываются значения ln(t _1/2), а по оси абсцисс - значения ln C ₀ (рис. 10), тогда n = - tga + 1.

Дифференциальный метод Вант-Гоффа.

Этот метод применяют, когда в реакции участвует одно вещество, или при участии нескольких веществ, когда все вещества, кроме данного (А), взяты в большом избытке. Тогда скорость реакции равна

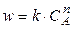. (21)

Прологарифмируем уравнение (21):

lnw = lnk + n lnС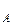

Очевидно, что в координатах lnw- lnC мы получим линейную зависимость, причем n = tga.

Построив зависимость lnw от lnC (рис. 11), можно определить порядок реакции, равный в данном случае тангенсу угла наклона прямой (n = tga).

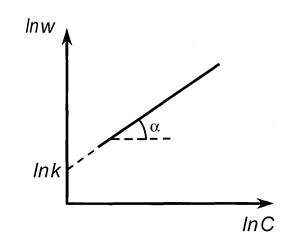
Рис. 11. Определение порядка реакции дифференциальным методом Вант-Гоффа.

Дата добавления: 2014-01-07