Основи побудови графів

ТЕМА 6. ОСНОВИ ТЕОРІЇ ГРАФІВ

Цілі і завдання вивчення теми: ознайомитись з основами теорії графів, засвоїти основні визначення та поняття, проаналізувати методику побудови матриць графів, та визначити область їх застосування.

Нескладний математичний апарат, який називають теорією графів, дає можливість ефективно розв'язувати, наприклад, аналіз транспорту, розміщення комунальних служб, постачання в будівництві, електричних ліній зв'язку, деякі задачі економіки та ін.

Геометрична наочність і простота основних понять та великий ступінь загальності, що дає можливість різноманітні задачі розглядати на однійграфовій моделі, обумовлюють широту практичних застосувань теорії графів.

Теорія графів — це розділ якісної геометрії, що почав бурхливо розвиватися па межі XIX—XX ст., особливо в 30-ті роки, коли була опублікована книга угорського вченого Д. Кеніга "Теорія скінчених і нескінчених графів" (Лейпціг, 1936).

Якісна геометрія, як відомо, оперує безрозмірними величинами. Тут не використовуються ні поняття кута і одиниць його виміру (градусів), ні довжини ліній (метрів, сантиметрів). Головне в якісній геометрії — наявність просторових елементів — точок, ліній, поверхонь, об'ємів і відношень (зв'язків) між ними. Основним поняттям теорії графів є поняття графа.

Граф — це множина X і множина відношень R, заданих на X. Графічно множина X зображається точками, що називаються вершинами графа, а множина R — лініями, так званими ребрами (дугами) графа. На рис.8 (а) точки 1, 2, 3,...,7— вершини графа, а лінії 1—2, 2—З, 2—4, 4—5, 2-—6 та ін. — його ребра.

Рис.8. Граф: неорієнтований (а), орієнтований (б), змішаний (в)

Ребро, яке з'єднує дві вершини графа, є інцидентним цим вершинам, а самі вершини — інцидентні ребру. Дві вершини графа іменуються суміжними; якщо вони визначають ребро графа. Два ребра іменуються суміжними, якщо вони мають спільну вершину. Вершина, інцидентна тільки одному ребру, називається висячою, а не інцидентна жодному ребру — ізольованою. Граф, утворений тільки ізольованими вершинами — це нуль-граф.

Якщо кінці ребра інцидентні одній і тій же вершині, то таке ребро називається петлею. На рис. 8 зображене ребро-петля, яке виходить з вершини 7 і входить у неї.

Інколи пари вершин з'єднуються не одним, а декількома ребрами. Такі графи називаються мультиграфами. Ними моделюються пари населених пунктів, що з'єднані декількома шляхами одного виду транспорту чи лініями декількох видів транспорту.

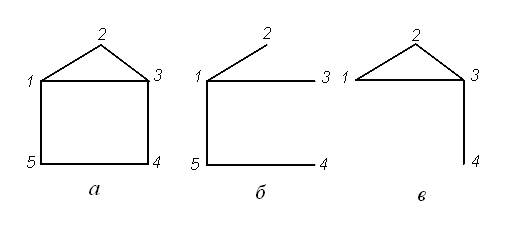
Рис. 9. Граф (а), його частковий граф (б), підграф (в)

Якщо порядок кінців ребер графа не береться до уваги, то такий граф називається неорієнтованим (рис. 8, а). У протилежному випадку, тобто коли пари вершин упорядковані, граф називається орієнтованим (орограф). Орієнтовані ребра — це дуги графа (рис. 8, б). Змішаним називається такий граф, в якому частина ребер орієнтована, а частина неорієнтована (рис. 8, б).

Графи бувають скінченими, якщо множина їхніх вершин X = {хі,х2,...,хп} є скінченою, і нескінченними, якщо ця множина змінюється від одиниці до нескінченності. В будівництві використовують положення теорії скінчених графів.

Якщо граф має п вершин (n > 1) і кожна пара вершин з'єднана ребром, він називається повним. У протилежному випадку маємо неповний граф.

Існують поняття.доповнення до графа, часткового графа і під-графа.

Доповнення до графа — це такий граф, ребра якого разом з цим графом утворюють повний граф (позначається через G).

Частковим називається граф, ребра якого є підмножиною цього графа і множина вершин якого збігається з множиною вершин цього графа (рис. 9, б).

Підграфом називається граф, вершинами якого є підмножина вершин певного графа, а ребрами — усі ребра, обидва кінці яких інцидентні цим вершинам (рис. 9, в). Так, граф на рис. 9 (б) є підграфом графа на рис. 9 (а), а цей останній є його надграфом.

Коли задається або відшукується певна послідовність ребер (дуг), тоді йдеться про маршрути— ланцюги і шляхи відповідно на неорієнтованому і орієнтованому графах, а також про цикли і контури теж відповідно на цих графах.

Ланцюг — така послідовність ребер неорієнтованого графа, в якій кінець одного ребра є початком іншого, а початкова і кінцева вершини не збігаються. Аналогічно визначається шлях на орографі. Перша у ланцюгу чи шляху вершина називається початковою, остання — кінцевою, всі інші — проміжними.

Ланцюги чи шляхи можуть бути простими і складними, елементарними і неелементарними. Прості вони в тому випадку, коли усі ребра (дуги) різні. В протилежному випадку — це складні ланцюги чи шляхи. Якщо у ланцюгу чи шляху жодна вершина не повторюється двічі, то він називається елементарним, і навпаки, ланцюг, який два або більше разів проходить через певну вершину, називається неелементарним.

Цикл — це ланцюг, який починається і закінчується однією і тією ж вершиною неорієнтованого графа. Аналогічно визначається контур орографа. Цикли і контури також бувають прості і складні, елементарні і неелементарні. Це залежить від виду ланцюгів, які їх утворюють.

На рис. 8, (а) маршрут 1-2, 2-6, 6-4, 4-5 є ланцюгом, а маршрут 1-2, 2-6, 6-4, 4-5, 5-1 — циклом. На рис. 8, (б) маршрут 1-2, 2-6, 6-4, 4-5 є шляхом. Цей же шлях плюс дуга 5-1 утворюють контур.

Виділяються також незалежні і залежні цикли чи контури. На рис. 8, а цикли 1-2, 2-4, 4-5, 5-1 та 2-6, 6-4, 4-2 незалежні, а цикл 1-2, 2-6, 6-4, 4-5, 5-1 залежний.

Ланцюг (шлях), цикл (контур) мають довжину, яка вимірюється кількістю ребер між початковою і кінцевою вершинами. Довжина ланцюга, що проходить через вершини 1-2-6-4-5 (рис. 8, а), дорівнює чотирьом, а довжина циклу 1-2-6-4-5-1 - п'ятьом.

Довжина найкоротшого ланцюга між певними двома вершинами графа називається відстанню між ними. Якщо для кожної вершини підрахувати відстань до найбільш віддаленої від неї вершини, то найменше з цих чисел називатиметься радіусом, а найбільше — діаметром графа.

Поняття ланцюга чи шляху вихідне для розуміння фундаментального поняття зв'язаності графа.

Дві вершини графа називаються зв'язаними, якщо існує ланцюг чи шлях з кінцями в цих вершинах. Тоді неорієнтований граф вважається зв'язаним, якщо будь-яка пара його вершин зв'язана.

Для орієнтованих графів існує поняття дуже і малозв'язаних графів. Дуже зв'язаний — це орограф, в якому для будь-якої пари вершин існує шлях, що з'єднує їх. У протилежному випадку орограф малозв'язаний.

Графом-деревом називається довільний зв'язаний граф, який не має циклів (див. рис. 9, б). Ребра такого графа іменуються вішками, а ребра графа — доповнення до цього графа-дерева — хордами.

Дата добавления: 2014-01-07