Матриці графів

Якщо граф має багато вершин і ребер, то він втрачає оглядовість. З таким графом важко працювати: у підрахунках трапляються помилки. Тоді відображають граф у вигляді матриці М. Найбільш поширеними є такі матриці графів: матриця суміжності відповідно вершин і ребер, матриця інциденті, матриця доступності, матриця відстаней. Накреслимо два графи (рис.10), відобразивши їх матричні еквіваленти.

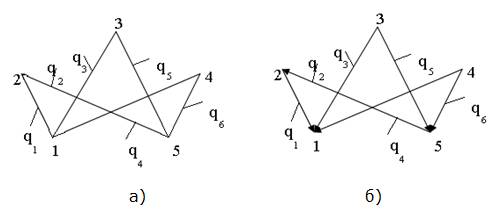
Рис.10. Неорієнтований (а) та орієнтований (б) графи з різними матрицями суміжності

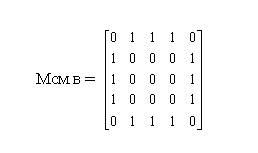
Матриця суміжності вершин графа Мсм.в - це квадратна матриця, в якій рядки і стовпчики відповідають вершинам графа. Порядок матриці збігається з кількістю вершин. При заповненні матриці на перетині рядка і стовпчика, що відповідають суміжним вершинам, ставлять 1; решту комірок заповняють нулями. Мсм вершин для графа(рис. 10, а) представлена такою таблицею:

Матриця суміжності ребер графа Мсм.р - це квадратна матриця, в якій рядки і стовпчики відповідають ребрам графа. Порядок матриці збігається з кількістю ребер. При заповненні матриці на перетині рядка і стовпчика, що відповідають суміжним ребрам, ставлять 1; решту комірок заповняють нулями. Мсм ребер для графа(рис. 10, а) представлена такою таблицею:

Матриця інциденції дуг графа Мін. – це ортогональна матриця, в якій стовпці відповідають вершинам графа, а рядки – ребрам. Матрицю заповнюють так: на перетині стовпчика, що відповідає певній вершині, з рядком, що відповідає ребру, яке з цієї вершини виходить, ставлять -1; з рядком, що відповідає ребру, яке в цю вершину входить, ставлять +1; з рядком, що відповідає ребру, яке неінцидентне даній вершині – 0. Мін. дуг для графа (рис. 10, б) представлена такою таблицею:

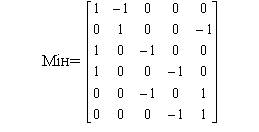
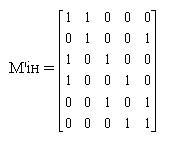
Матриця інциденції ребер графа Мін. – це ортогональна матриця, в якій стовпці відповідають вершинам графа, а рядки – ребрам. Матрицю заповнюють так: на перетині стовпчика, що відповідає певній вершині, з рядком, що відповідає ребру, якому ця вершина інцидентна, ставлять + 1; решту комірок заповнюють нулями. Мін. ребер для графа (рис. 10, а) представлена такою таблицею:

Матриці суміжності та інциденції визначають графи з точністю до ізоморфізму. За цими матрицями можна точно накреслити ізоморфні їм графи.

Матриця доступності графа Мд. – це квадратна матриця, в якій рядки і стовпчики відповідають вершинам графа. Матрицю заповнюють так: на перетині рядка і стовпчика ставлять 1, якщо j-та вершина доступна з i-ї, решту комірок заповнюють нулями. Для зв’язаного неорієнтованого графа всі елементи Мд рівні 1. У Мд орографа частина елементів може дорівнювати нулеві. Це засвідчує така матриця, ізоморфна графу (рис. 10, б):

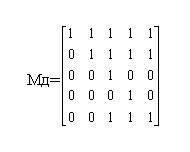
Часто елементами Мд є топологічні відстані від i-тої до j-тої вершини, тобто кількість ребер за найкоротшим ланцюгом.

Матриця відстаней графа Мв - це квадратна матриця, в якій рядки і стовпчики відповідають вершинам графа. Її елемент показує відстань від i-тої до j-тої вершини, виміряну кількістю ребер (дуг) за найкоротшим маршрутом. Якщо в орографі шлях від вершини відсутній, то відстань дорівнює нескінченності. Матриця відстаней орографа (рис. 10, б) має такий вигляд:

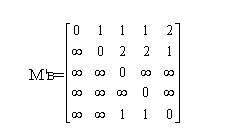
Аналогічно визначається матриця відстаней неорієнтованого графа, хоч тут нескінченні відстані відсутні.

Матриця циклів графа Мц. У цій матриці кожному незалежному циклові відводиться рядок, а кожному ребру – стовпчик. Матрицю заповнюють так: на перетині стовпчика, що відповідає певному ребру, з рядком, що відповідає циклу, який має дане ребро, ставлять 1; решту комірок заповнюють нулями.

На відміну від матриць суміжності і матриць інциденції, матриця циклів не визначає графа з точністю до ізоморфізму.

Питання для самоперевірки:

1. Що розуміють під терміном „граф ”?

2. Які вершини графа називаються суміжними?

3. Дайте визначення поняттю „ланцюг графа”?

4. Дайте визначення поняттю „мультиграф”?

5. Дайте визначення поняттю „інцидентність”?

6. Які графи називаються орієнтованими?

7. Дайте визначення поняттю „цикл графа”?

Резюме по темі:

Теорія графів — це розділ якісної геометрії, що почав бурхливо розвиватися па межі XIX—XX ст., особливо в 30-ті роки, коли була опублікована книга угорського вченого Д. Кеніга "Теорія скінчених і нескінчених графів" (Лейпціг, 1936).

Якісна геометрія, як відомо, оперує безрозмірними величинами. Тут не використовуються ні поняття кута і одиниць його виміру (градусів), ні довжини ліній (метрів, сантиметрів). Головне в якісній геометрії — наявність просторових елементів — точок, ліній, поверхонь, об'ємів і відношень (зв'язків) між ними. Основним поняттям теорії графів є поняття графа.

Якщо граф має багато вершин і ребер, то він втрачає оглядовість. З таким графом важко працювати: у підрахунках трапляються помилки. Тоді відображають граф у вигляді матриці М. Найбільш поширеними є такі матриці графів: матриця суміжності відповідно вершин і ребер, матриця інциденті, матриця доступності, матриця відстаней.

Дата добавления: 2014-01-07