Вероятностное толкование волн де Бройля

Волновая функция и волна де Бройля

Формула Эйлера и комплексная формула записи волн.

Волны де Бройля и волновая функция.

S (x,t) = aCos (ωt – kx +σ)

ωt – kx + σ = α

Формула Эйлера: e^{+-i α} = Cos α +- iSin α

Для p – x iSin α = 0

aCos α = a e^{+-i α}

S(x,t) = a e^{+-i α}

Пси функция обусловлена колебанием волны в пространстве

Ψ(x,t) = a e^{+-i α}

Ψ(x,t) = a e^{+-i (ωt – kx +σ)} = ae ^{+-i σ} e^{+-i (ωt – kx)}

ae ^{+-i σ} =A

ωt – kx = (Et - px)(1/ ħ)

Ψ(x,t) = Ae^{-i(1/ ħ) (Et - px)} для свободной мкч

Ψ ψ

Ψ(x,t) = A e^{–i(ωt –kr)} =Ae ^{–(1/ħ)(Et - pr)} - свободная мкч

Ψ(r,t) = A e^{–i/ ħ (Et –pr)} = A e^{–i/ ħ (kEt –PxX – PyY - PzZ)}

Ψ(x,t) = A(x,t) e^{–i/ ħ (Et –pt)}

Прохождение мкч через кристалл

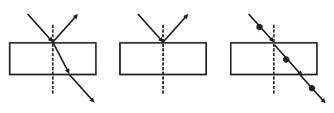
Или отражается или проходит.

W – вероятность: | Ψ (x,t)|²

Мысленный интерференционно - дифференционный опыт:

Две щели, на них направлен поток электронов и ставится фотопластинка. Там куда попадают электроны пленка темнеет. Время экспозиции τ.

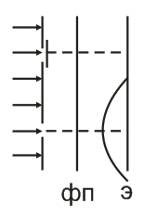
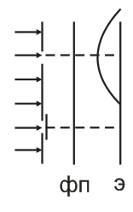
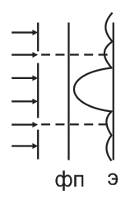
Щели поочередно открывают.

Если поток сделать очень слабым, то картина сохранится (опыт фабрикана)

Электрон «чувствует» какая щель открыта, обе щели действуют на него. Электрон пройдет только через 1 щель. Движением мкч управляют волновые свойства.

Вероятность попадания электрона в щель:

| Ψ |² dV (объем)

| Ψ |² = dW/dV – плотность вероятности

| Ψ (x,y,z,t) |² = dW/dV – плотность вероятности обнаружить мкч в точке с координатами x,y,z в момент времени t

Ψ (x,y,z,t) = A e^{–i/ ħ (Et –pr)}

| Ψ (x,y,z,t) |² = Ψ (x,y,z,t) Ψ*(x,y,z,t)

Ψ*(x,y,z,t) – комплексная сопряженная

Плотность вероятности – вероятность, отнесенная к единице объема.

В квантовой механике движение 1й мкч уже связано с W

1 частица имеет вероятностный характер.

§8 Вероятность нахождения мкч.Нахождение средних значений функции от координат. (роль Ψ –фунукции в квантовой механике)

Ψ(x,t) = A e^{–i/ ħ (Et –px)}

| Ψ(x,t) |² = dW/dV

dW = | Ψ(x,t) |² dV

W = (интеграл от x1 до x2)(Ψ*(x,t) Ψ(x,t)dx)

Условие нормировки:

(интеграл от – бесконечности до + бесконечности) (| Ψ(x,t) |² dx) =1 одномерный случай

(3 интеграла от – бесконечности до + бесконечности)(Ψ*(x,y,z,t) Ψ(x,y,z,t)dxdydz) = 1

Плоская волна де Бройля не нормируется на единицу:

Свободная мкч

Ψ(x,t) = A e^{–i/ ħ (Et –px)}

| Ψ(x,t) |² = A e^{–i/ ħ (Et –px)} A e^{–i/ ħ (Et –px)} = A²

(интеграл от – бесконечности до + бесконечности) (| Ψ(x,t) |² dx) стремится к бесконечности

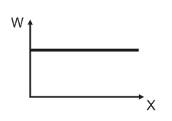
Непрерывна однозначна конечна!

Нахождение средних значений координаты и функции от координат.

<F(x)> = (интеграл от – бесконечности до + бесконечности) (F(x)W(x)dx)

Здесь W(x) – плотность вероятности, d(x) – класс статист.

(интеграл от – бесконечности до + бесконечности) (W(x)dx) = 1

В квантовой механике:

(интеграл от – бесконечности до + бесконечности) (Ψ(x,t)* f(x) Ψ(x,t) dx) =

(интеграл от – бесконечности до + бесконечности) (|Ψ(x)²| f(x) dx) =

(интеграл от – бесконечности до + бесконечности) (Ψ*(x,t) Ψ(x,t) dx) = 1

<f (x,y,z)> = (3 интеграла от – бесконечности до + бесконечности)(Ψ*(x,y,z,t) f(x,y,z)Ψ(x,y,z,t)dxdydz)= (3 интеграла от – бесконечности до + бесконечности)(|Ψ(x,y,z,t)|² dxdydz)=1

Глава 5. Уравнение Шредингера.

Дата добавления: 2014-01-07