
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Символи граней
|
|
|
|
Всі шість величин a, b, c і α, β, γ визначають форму і розміри паралелепіпеда гратки. Відношення a: b: c і осьові кути α, β, γ називаються константами даної кристалічної речовини. Для різних сингоній константи перебувають у такому співвідношенні:
Триклинна сингонія a ≠ b ≠ c, α ≠ β ≠ γ ≠ 90°;
Моноклінна сингонія a ≠ b ≠ c, α = γ = 90°; β ≠ 90°;
Ромбічна сингонія a ≠ b ≠ c, α = β = γ = 90°;
Тригональна сингонія a = b = c, α = β = γ ≠ 90°;
Тетрагональна сингонія a = b ≠ c, α = β = γ =90°;
Гексагональна сингонія a = b ≠ c, α = β = 90°, γ ≠ 120°;
Кубічна сингонія a = b = c, α = β = γ = 90°;
Положення будь-якої грані кристала в просторі може бути зображено згідно із законом цілих чисел. Зокрема, вибравши певну систему відліку, можемо зафіксувати в просторі положення будь-якої грані за допомогою трьох числових параметрів. Наприклад, для грані A 2 B 2 C 2 (Рис. 1) відношенням таких параметрів буде 2 a: 3 b: 6 c. Таке позначення грані називається індексуванням за Вейссом. Цей спосіб індексів незручний, тому на практиці застосовують інший – спосіб Міллера, який заснований на заміні вейссівських параметрів оберненими до них величинами. Так в наведеному вище прикладі беруть участь не числові параметри 2: 3: 6, а обернені до них величини: 1/2: 1/3: 1/6. Зберігаючи співвідношення, їх можна привести до цілих чисел 1/2: 1/3: 1/6 = 3: 2: 1. Ці числа позначають h: k: l (h: k: l = 3: 2: 1). Числа h, k, l називають індексами грані. Записані підряд індекси і взяті в прості круглі дужки (h k l) – це символи грані. Таким чином, символом грані називається сукупність трьох найменших чисел, які обернено пропорційні числовим параметрам даної грані. Якщо грань кристала розміщена відносно початку відліку так, що перетинає від’ємний напрям координатної осі, то індекси Міллера цієї грані визначаються таким самим способом, лише над відповідним індексом ставиться знак «−». Наприклад: грань перетинає від’ємний напрям осі x і додатні напрями осей yz. Отже, символом такої грані буде (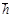 k l). За умови, що грань паралельна до однієї або до двох координатних осей, вейссівські параметри її по цих осях прямують до ∞. В індексах Міллера число 0 означає паралельність даної грані до відповідної осі. Так, символ (h k 0) вказує, що дана грань є паралельною до осі z. У випадку, коли грань перпендикулярна до певної осі (наприклад, до осі x), немає потреби записувати її символ (h 0 0), бо така грань завжди може бути перенесена паралельно сама собі і її символ буде (1 0 0). Для прикладу на Рис. 2 показано індекси окремих граней та діагональних площин куба.
k l). За умови, що грань паралельна до однієї або до двох координатних осей, вейссівські параметри її по цих осях прямують до ∞. В індексах Міллера число 0 означає паралельність даної грані до відповідної осі. Так, символ (h k 0) вказує, що дана грань є паралельною до осі z. У випадку, коли грань перпендикулярна до певної осі (наприклад, до осі x), немає потреби записувати її символ (h 0 0), бо така грань завжди може бути перенесена паралельно сама собі і її символ буде (1 0 0). Для прикладу на Рис. 2 показано індекси окремих граней та діагональних площин куба.
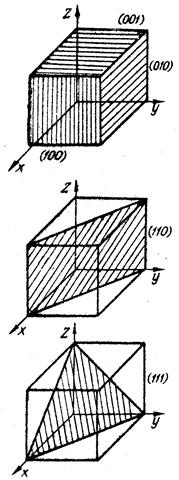
Рис. 2. Індекси граней та діагональних площин куба.
Положення в просторі будь-якої грані кристала можна виразити не лише за допомогою відрізків на координатних осях, а й за допомогою кутів між координатними осями і нормаллю OP, проведеною з початку координат до грані ABC. З Рис. 3 видно, що
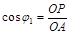 ,
, 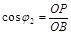 ,
, 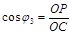 (2)
(2)
Відношення цих косинусів запишеться так:
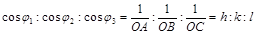 (3)
(3)
Одержані числа h, k, l – обернено пропорційні осьовим відрізкам і відповідають індексам Міллера.
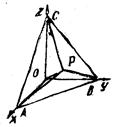
Рис. 3. Визначення індексів Міллера.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 542; Нарушение авторских прав?; Мы поможем в написании вашей работы!