Закон поясів

Сукупність граней кристала, які перетинаються між собою по паралельних ребрах, називається поясом. Лінія, яка паралельна до таких ребер і проходить через початок координат, називається віссю пояса.

Закон поясів базується на таких положеннях:

1. Всяка площина, паралельна двом дійсним або можливим ребрам кристала, є дійсною або можливою гранню кристала.

2. Всякий напрям, паралельний до лінії перетину двох дійсних або можливий граней кристала, завжди є дійсним або можливим ребром кристала.

Ряд або вузлова пряма у гратці, а також ребро кристалічного багатогранника в обраній

системі координат для даної кристалічної речовини позначається як і грань, трьома або чотирма (в тригональній і гексагональній сингоніях) цілими числами, які називаються індексами ребра. Якщо ряд не проходить через початок координат, то його можна перенести паралельно самому собі до проходження через початок координат. Така операція цілком правомірна, тому що всі паралельні напрями в кристалі рівнозначні.

Ряд, що проходить через початок координат, характеризується двома точками: початком координат і будь-яким вузлом ряду. Кожен вузол у гратці описується трьома числами r ₁, r ₂, r ₃, які називають індексами вузла. Сукупність цих чисел записаних у подвійних квадратних дужках [[ r ₁ r ₂ r ₃]], називається символом вузла. Звідси випливає, що будь-який вузол, що належить до даного ряду, характеризує цей ряд своїм символом. Таким чином, як символ ряду беруть символ вузла у вигляді [ r ₁ r ₂ r ₃].

Рис. 4. Визначення символів вузлів та ребер.

Так, з Рис. 4 видно, що:

(4)

Звідси символом ребра OC буде [1 2 3]. Символ грані (h k l) і розміщеного в ній ряда (ребра) [ r ₁ r ₂ r ₃] зв’язані залежністю:

hr ₁ + kr ₂ + lr ₃ = 0 (5)

Ця залежність доводиться на основі рівнянь площини і прямої, що лежать у цій площині. Площина, яка проходить через початок координат описується рівнянням:

hx + ky + lz = 0 (6)

Якщо пряма міститься в даній площині, то координати довільної точки прямої повинні задовольняти рівнянню (6). Підставляючи у це рівняння значення x = r ₁, y = r ₂, z = r ₃, одержимо рівність (5).

Залежність (5) дає змогу розв’язувати ряд практичних задач практичної кристалографії:

1. З визначення пояса відомо, що всі його ребра паралельні, тобто мають однакові символи [ r ₁ r ₂ r ₃].

Скористаємось співвідношенням (5), щоб знайти якусь характерну ознаку символів граней певного пояса. Візьмемо пояс [1 1 1]. Підставляючи значення r ₁, r ₂, r ₃ у рівняння (5), одержимо

1 h + 1 k + 1 l = 0,

тобто

h + k + l = 0.

Звідси можна зробити висновок, що всі грані, сума індексів яких дорівнює нулю, належать до пояса [1 1 1].

Для пояса [0 0 1] отримаємо:

0 h + 0 k + 1 l = 0,

Звідси l = 0. Висновок: поясу [0 0 1] належать всі грані, які мають третій індекс, рівний нулю, і т.д.

2. Нехай дві грані (h ₁ k ₁ l ₁) і (h ₁ k ₁ l ₁) перетинаються вздовж ребра [ r ₁ r ₂ r ₃]. Потрібно зобразити (знайти) індекси цього ребра через відомі індекси граней. Для цього необхідно розв’язати рівняння:

h ₁ r ₁ + k ₁ r ₂ + l ₁ r ₃ = 0 (7)

h ₂ r ₁ + k ₂ r ₂ + l ₂ r ₃ = 0

Розв’язавши ці рівняння, отримаємо:

r ₁: r ₂: r ₃ = (k ₁ l ₂ − l ₁ k ₂): (l ₁ h ₂ − h ₁ l ₂): (h ₁ k ₂ − k ₁ h ₂) (8)

Двочлени в правій частині рівняння (8) є детермінантами

k 1	l 1
k 2	l 2

;

k 1	l 1
k 2	l 2

;

k 1	l 1
k 2	l 2

(9)

Які одержують з матриці (10):

h 1	k 1	l 1
h 2	k 2	l 2

За схемою (12):

h 1	k 1		l 1		h 1		k 1	l 1
		×		×		×
h 2	k 2		l 2		h 2		k 2	l 2

З цього випливає, що символ ребра, вздовж якого перетинаються дві грані з відомими індексами, можна легко визначити за допомогою такого прийому. Двічі записують індекси двох граней у двох рядках (12). У такому записі крайні стовпчики відкидаються і здійснюється перехресне множення та береться різниця сусідніх добутків, результати яких і будуть мати зміст індексів ребра.

Наприклад дано дві грані з індексами (3 2 0) і (1 1 0). Необхідно знайти символ ребра, вздовж якого ці грані перетинаються. Запишемо умову 12:

		×		×		×

З неї випливає, що r ₁ = 0, r ₂ = 0, r ₃ = 3 × 1 – 2 × 1 = 1, тобто [ r ₁ r ₂ r ₃] = [0 0 1].

Використовуючи умову (12), можна розв’язати таку задачу. Відомі символи двох ребер (наприклад, [-1 2 0] і [1 2 2]). Необхідно знайти символ грані, в якій ці ребра містяться одночасно. Визначимо символ такої грані:

–1					–1
		×		×		×

Враховуючи зміст індексів Міллера для грані, запишемо:

1/ h = 2 × 2 – 2 × 0 = 4, 1/ k = 1 × 0 – 2 × (–1) = 2, 1/ l = 2 × (–1) – 2 = –4,

,

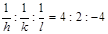звідси (h k l) = (1 2 ).

3. Зазначимо ще таке важливе правило. Додаючи відповідні індекси двох граней, отримаємо символ нової грані пояса. Віссю його є напрям ребра, вздовж якого перетинаються взяті грані. Таким чином, на основі деякої кількості відомих граней кристала можна побудувати всі можливі його грані та визначити їх символи.

Дата добавления: 2014-01-07