Спектральне уявлення періодичних та неперіодичних сигналів

Спектри періодичних послідовностей.

Спектральне уявлення періодичних та неперіодичних сигналів.

Тема: Спектральне уявлення періодичних сигналів.

Суспільна роль місцевих бюджетів

В державних фінансах:

- складова бюджетної системи;

- інструмент реалізації загальнодержавних програм;

- джерело фінансування державних видатків;

- інструмент фінансового вирівнювання

В місцевих фінансах:

- фінансова база місцевого самоврядування;

- фінансові плани територіальних формувань;

- джерело утримання і розвитку місцевого господарства;

- джерело фінансування локальних послуг

в економічній системі держави

Впливають:

- на соціально-економічний розвиток;

- фінансову безпеку;

- фінансову стабільність;

- розвиток демократії;

- добробут населення

Використовуються як інструмент:

- перерозподілу ВВП;

- державного регулювання на мікрорівні;

- регіональної політики;

- фінансової політики;

- економічної політики

Зміст

Знайдемо амплітудний спектр прямокутного імпульсу описаного за допомогою функцій включення l(t): 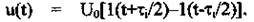Для знаходження спектру використовується пряме перетворення Фур'є, яке для випадку, коли сигнал має вигляд парної функції, можна записати наступним чином:

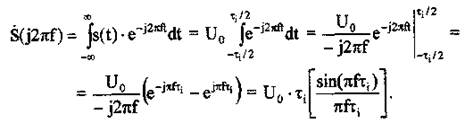
Застосувавши для перетворення виразу для S(j2?tf) формулу Ейлера: 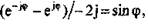отримаємо вираз для комплексної спектральної густини

у вигляді функції типу (sin x)/x.

Комплексна спектральна густина зображується на т.зв. спектральних діаграмах у вигляді амплітудного S(ω) та фазового ψ(ω) спектрів. Для прямокутного відеоімпульсу, парного відносно t = 0 S(ω) і ψ(ω) дорівнюють відповідно:

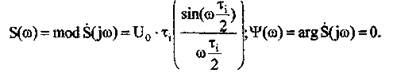
Внаслідок парності функції U(t) функція S(jω) виходить дійсною, тому фазовий спектр дорівнює нулю.

Приймемо, що U₀=3 В; τ_і = 1 мс. Тобто, включення сигналу відбувається в момент часу t = -τ_і/2 = -0,5 мс, а його виключення, - в момент часу t = τ_і/2 = 0,5 мс.

Амплітудний спектр

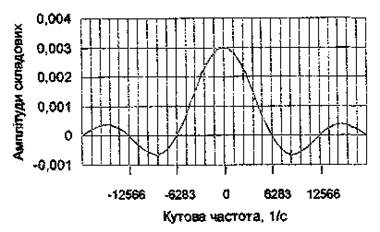
Підставивши числові значення величин, отри­муємо для амплітудного спектру вираз:

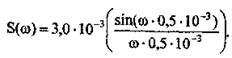
Ширина спектру сигналу F_s визначається як F_s = f_max-f_min. для прямокутного імпульсу ширина спектру пов'язана з розміщенням на осі частот т.зв. нулів обвідної - значень частоти, при яких амплітуди складових спектру завжди дорівнюють нулю. Часто за верхню межу спектру сигналу приймають частоту першого нуля спектру, бо там буває зосереджено основну енергію сигналу (95%). Нулі обвідної можливо знайти за умови, що функція (sin x)/x перетинає вісь ω при ωτ_і/2 = ±nπ, або ω = ±2nπ/τ_і. Для трьох пелюсток спектру в даній задачі нулями обвідної будуть частоти:

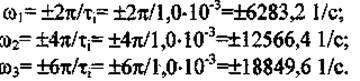
Як бачимо, розміщення нулів обвідної залежить тільки від тривалості імпульсу τ_і.

Дата добавления: 2014-01-07