Мал. 4

Вершина називається шарніром (або точкою зчленування), якщо при її видаленні число компонент зв'язності збільшується. У графа на мал. 4 є чотири шарніри - це вершини .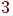

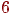
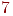
Ребро, при видаленні якого збільшується число компонент зв'язності, називається перешийком. Перешийками графа, зображеного на мал. 4 є ребра .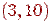

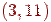
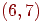
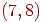
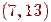Граф 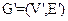є частиною графа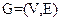, якщо і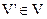 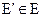. Частина графа, яка разом з деякою підмножиною ребер графа, містить всі інцидентні ним вершини, називається підграфом. Частина графа, яка разом з деякою підмножиною ребер графа, містить всі вершини графа, називається (,)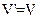 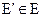називається суграфом.

Початковий граф по відношенню до його підграфа називається надграфом, а по відношенню до суграфу - надграфом. Сукупність всіх ребер графа, що не належать його підграфові, утворює доповнення підграфа. Говорять, що підграфи і розділені ребрами, якщо вони не мають загальних ребер () і розділені вершинами, якщо вони не мають загальних вершин ().

Два графи G(V, E) і H(W, I) називаються ізоморфними, якщо існує взаємно-однозначна відповідність між безліччю вершин V, W і безліччю ребер E, I, що зберігає відношення інцидентності. Можна сказати, що ізоморфні графи – це один і той же граф, в якому вершини названі по-різному.

Цикл – це замкнутий ланцюг, тобто замкнутий маршрут, в якому кожне ребро використовується не більше одного разу. Гамільтоновим називається цикл, що проходить по кожній вершині графа рівно один раз. Цикл Ейлеров – цикл графа, що містить всі його ребра.

Маршрут, що містить всі вершини або ребра графа і що володіє певними властивостями, називається обходом графа.

Довжина маршруту (ланцюги, простій ланцюги) рівна кількості ребер в порядку їх проходження. Довжина найкоротшою простій ланцюгу, що сполучає вершини vi і vj в графові G, називається відстанню d (vi, vj) між vi і vj. У зв'язному неорієнтованому графові відстань задовольняє аксіомам метрики.

За допомогою різних операцій можна будувати графи простіших, переходити від графа до простішому, розбивати графи простіші і так далі Серед одномісних операцій найбільш споживані: видалення і додавання ребра або вершини, стягання ребра (ототожнення пари суміжних вершин), підрозбиття ребра (тобто заміна ребра (u, v) на пару (u, w), (w, v), де w - нова вершина) і ін. Відомі двомісні операції: з'єднання, складання, різні види множень графів і ін. Такі операції використовуються для аналізу і синтезу графів із заданими властивостями.

Деякі види графів мають спеціальні назви. Повним графом називається неорієнтований граф, що містить всі можливі ребра для даної безлічі вершин (будь-яка вершина суміжна будь-який інший). Неорієнтований граф називають дводольним, якщо безліч вершин V можна розбити на дві частини V1 і V2 таким чином, що кінці будь-якого ребра опиняються в різних частинах. Зупинимося докладніше на основному для теорії алгоритмів класі графів - деревах.

Граф без циклів називається ациклічним. Ациклічний зв'язковий граф називається деревом. Довільний ациклічний граф називається лісом.

Контрольні запитання:

1. Дати визначення графа.

2. Які бувають графи.

3. Дати визначення орграфа.

4. Зв’язність і компоненти графа.

Література

1. Ахи А., Хопкрофт Д., Ульман Д. Структуры данных и алгоритмы.: Пер. с англ. М.: Издат. дом «Вильямс», 2000. С. 183–225

2. Кормен Т., Лейзерсон Ч., Ривест Р.., Алгоритмы: построение и анализ: Пер. с англ., М.: МЦНМО, 2001. С. 88–91, 435–523

3. Седжвик Р. Фундаментальные алгоритмы на С. Анализ/Структуры данных/Сортировка/Поиск/Алгоритмы на графах: Пер. с англ. СПб.: «ДиаСофтЮП», 2003. С. 673–1000

Дата добавления: 2014-01-07