
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оцінювання ймовірності
|
|
|
|
Припустимо, що метою моделювання є оцінювання ймовірності настання деякої події А, яка визначає стан системи. У кожній з N реалізацій процесу настання події А є випадковою величиною 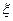 , що набуває значення
, що набуває значення 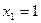 з імовірністю
з імовірністю 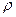 і
і 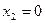 з імовірністю
з імовірністю 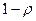 . Тоді можна визначити математичне сподівання і дисперсію відповідно за формулами
. Тоді можна визначити математичне сподівання і дисперсію відповідно за формулами
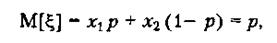 (2.2)
(2.2) 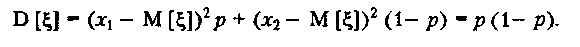 (2.3)
(2.3)
Як оцінку 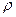 використовують частість настання події А. Ця оцінка є незміщеною, спроможною та ефективною. За умови, що N задано, для отримання цієї оцінки достатньо накопичувати m:
використовують частість настання події А. Ця оцінка є незміщеною, спроможною та ефективною. За умови, що N задано, для отримання цієї оцінки достатньо накопичувати m:
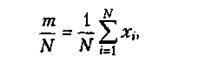 (2.4)
(2.4)
де 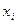 - настання події А в реалізації і.
- настання події А в реалізації і.
За формулами (2.2)-(2.4) визначимо вибіркове математичне сподівання
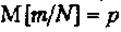 і дисперсію
і дисперсію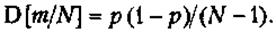
Згідно з центральною граничною теоремою (у даному випадку її можна взяти у вигляді теореми Хінчина) випадкова величина m/N буде мати розподіл, близький до нормального (рис. 1). Тому для кожного рівня достовірності 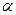 з таблиць нормального розподілу можна знайти таку величину
з таблиць нормального розподілу можна знайти таку величину 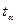 , при якій точність обчислюватиметься за формулою
, при якій точність обчислюватиметься за формулою
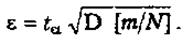 (2.5)
(2.5)
Якщо 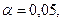 то
то 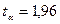 , а якщо
, а якщо 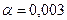 , то
, то 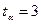 . Підставимо у формулу (2.5) вираз дисперсії:
. Підставимо у формулу (2.5) вираз дисперсії:
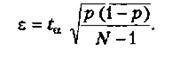
Звідси
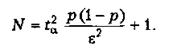 (2.6)
(2.6)
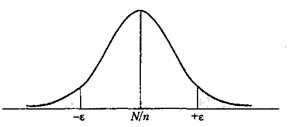
Рис. 1. Функція нормального розподілу для побудови довірчого інтервалу
З формули (2.6) видно, що при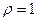 ,або
,або 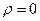 кількість реалізацій, які необхідно провести для підтвердження того, що подія А настає (або ні), дорівнює одиниці. Але оскільки ймовірність
кількість реалізацій, які необхідно провести для підтвердження того, що подія А настає (або ні), дорівнює одиниці. Але оскільки ймовірність 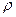 заздалегідь невідома, провадять випробування (N= 50... 100), оцінюють частість m/N і підставляють її значення у вираз (2.6) замість
заздалегідь невідома, провадять випробування (N= 50... 100), оцінюють частість m/N і підставляють її значення у вираз (2.6) замість 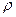 , після чого визначають остаточну кількість реалізацій. Графік залежності числа реалізацій для
, після чого визначають остаточну кількість реалізацій. Графік залежності числа реалізацій для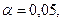 і різних значень
і різних значень 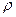 , якщо
, якщо 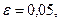 , наведено на рис. 2.
, наведено на рис. 2.
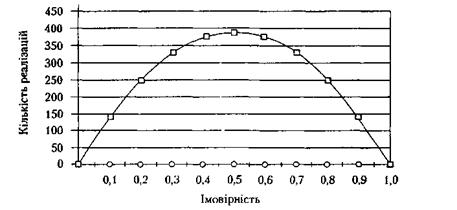
Рис. 2. Залежність числа реалізацій від значень імовірності
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 480; Нарушение авторских прав?; Мы поможем в написании вашей работы!