Вектор кутової швидкості. Формула Ейлера

Леонард Ейлер (1707-1783) – видатний швейцарський вчений, який довгий час працював у Росії (1727-1741 і 1766-1783) і Германії (1741-1766). До його пера належать біля 850 наукових праць, з яких 550 були опубліковані. Найбільш відомі наступні його роботи:

· "Механіка, або Наука про рух, викладена аналітично" (1736);

· "Вступ до аналізу" (1748);

· "Диференціальне числення" (1755);

· "Теорія руху твердого тіла" (1765);

· "Універсальна арифметика" (1768-1769);

· "Інтегральне числення" (1768-1794).

Нехай маємо тіло, що обертається з кутовою швидкістю 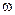(див. рис. 2.6). Зв'яжемо жорстко з цим тілом систему координат 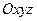. Визначимо швидкість точки 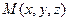тіла, для чого з'єднаємо її з початком координат радіус-вектором 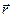, тоді

.

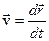Розкладемо радіус-вектор 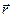за ортами системи координат :

.

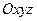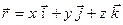(2.16)

Продиференціюємо вираз (2.16), врахувавши, що координати 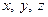та орт 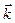- сталі, а змінними у часі є орти :

.

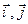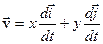(2.17)

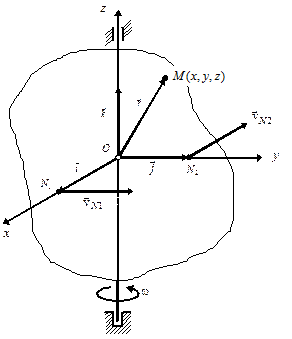
Рис. 2.6. До виводу формули Ейлера.

Знайдемо похідн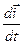і і 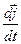. Зауважимо, що 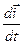- це швидкість точки 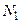кінця орта 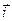, яка окреслює годограф орта 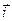, тобто

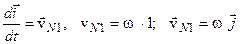(оскільки до осі )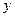

тоді

.

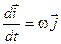(2.18)

Аналогічно

(),

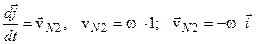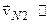
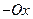тобто

.

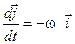(2.19)

В цьому разі маємо

.

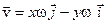(2.20)

Врахуємо, що орти 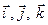легко виражаються один через другий:

.

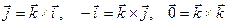Підставляючи ці співвідношення у формулу (2.20), отримаємо:

,

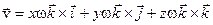або

,

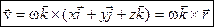(2.21)

де

.

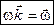(2.22)

Висновок: із формули (2.22) випливає, що кутова швидкість - це вектор, який лежить на осі обертання і напрямлений у ту частину простору, звідки обертання тіла видно як таке, що відбувається проти ходу годинникової стрілки.

Тоді маємо співвідношення

,

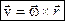(2.23)

яке являє собою формули Ейлера. У проекціях на осі системи координат 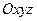цю формулу у загальному випадку можна записати так:

.

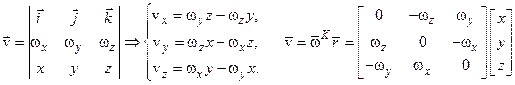(2.24)

У разі, коли вісь 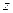- нерухома (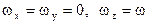), маємо:

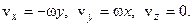
Визначимо вектор кутового прискорення

.

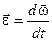Вектор 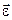напрямлений по дотичній до годографа вектора 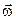. А оскільки у даному разі годографом вектора 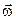є сама вісь обертання, то вектор 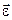, як і 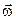, напрямлений по ній (див. рис. 2.7).

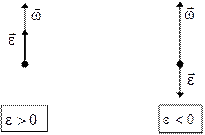
Рис. 2.7. До визначення напрямку вектора кутового прискорення.

Приклад. Виведемо рівняння рівнозмінного обертання тіла навколо осі.

У цьому випадку , але 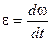, тоді

.

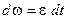Інтегруючи це рівняння за часом, отримаємо

.

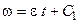Якщо при 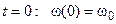, то тоді 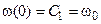, і маємо

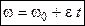
(2.25)

- закон зміни кутової швидкості при рівнозмінному обертанні.

Далі, оскільки 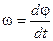, то 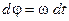і, інтегруючи цей вираз за часом, отримаємо

.

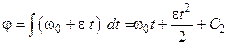Якщо при 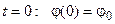, то тоді 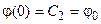, і отримаємо

.

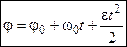(2.26)

- рівняння рівнозмінного обертання АТТ навколо нерухомої осі.

Дата добавления: 2014-01-07; Просмотров: 926; Нарушение авторских прав?; Мы поможем в написании вашей работы!