
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Последовательные реакции
|
|
|
|
Последовательные (или консекутивные) реакции – это реакции, протекающие одна за другой, то есть реакции с промежуточными стадиями. Таких реакций большинство, однако характер промежуточных веществ не всегда удается установить из-за экспериментальных трудностей.
Рассмотрим сначала наиболее простой случай двух последовательных мономолекулярных реакций, когда из 1 моль вещества А образуется 1 моль вещества В, а из 1 моль вещества В образуется 1 моль вещества С.
Пусть в начальный момент времени имеется а моль вещества А. К моменту t: осталось (a – x) моль вещества А,
появилось (x – y) моль вещества В,
появилось у моль вещества С.
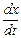 = k 1 (a – x).
= k 1 (a – x).
После интегрирования (см. необратимые реакции 1-го порядка) получим
a – x = а  .
.
Скорость превращения вещества В равна
 = k 1 (a – x) – k 2 (x – y) = k 1 а
= k 1 (a – x) – k 2 (x – y) = k 1 а  – k 2 (x – y),
– k 2 (x – y),
 + k 2 (x – y) = k 1 а
+ k 2 (x – y) = k 1 а  .
.
Решив это дифференциальное уравнение, будем иметь
x – y = а 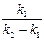 (
( –
–  ),
),
y = a (1 – 
 +
+ 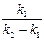
 ).
).
Покажем эти кривые на рис. 3. Кривая (х – у) изменения количества промежуточного вещества В во времени имеет максимум при t max, при котором получается наибольшее количество вещества В. Значение t max найдем из условия
 = 0.
= 0.
 = a
= a 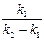 (– k 1
(– k 1 + k 2
+ k 2 ) = 0,
) = 0,
k 1 = k 2
= k 2 .
.
Логарифмируем
ln k 1 – k 1 t max = ln k 2 – k 2 t max,
t max =  .
.
Пусть k 2 / k 1 = r, то есть k 2 = k 1 r: t max = 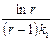 . Подставим это выражение для t max в уравнение для (х – у):
. Подставим это выражение для t max в уравнение для (х – у):
(х – у)max =  (
( –
– 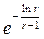 ).
).

| Рис. 3. Кинетические кривые для последовательной реакции первого порядка |
Наибольшее количество промежуточного вещества В зависит не от абсолютных значений скоростей обеих реакций, а только от отношения этих скоростей. Чем больше k 2 / k 1, тем больше ордината максимума на кривой (х – у) = f (t) и тем ближе этот максимум к началу реакции.
Кривая у = f ( t ), характеризующая накопление конечного продукта С во времени, имеет точку перегиба. Точка перегиба совпадает с точкой максимума на кривой (х – у) = f (t). Точка перегиба на кривой у = f (t) указывает на то, что вещество С образуется с начальным ускорением. Расчеты показывают, что при малых значениях отношения k 1 / k 2 кривая у вначале практически совпадает с осью абсцисс, то есть вещество С в течение некоторого промежутка времени после начала реакции аналитически обнаружить нельзя. Этот промежуток времени получил название периода индукции.
Если k 1 < k 2, то через достаточно большой промежуток времени
 <<
<< 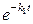 .
.
Тогда x – y = а 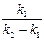
 ; а
; а  = а – х.
= а – х.
Þ x – y =  или
или  =
= 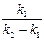 .
.
Таким образом, отношение количеств веществ В и А через определенный промежуток времени после начала реакции становится постоянным и в течение некоторого промежутка времени практически не изменяется. Другими словами, количество веществ А и В убывает в одинаковой степени. Такое состояние называется переходным равновесием.
Если k 1 << k 2, то  =
= 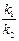 =
= 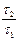 (t2, t1 – времена полураспада веществ В и А). Равновесие, отвечающее этому уравнению, называется вековым. Кроме того, при k 1 << k 2 уравнение для у принимает вид:
(t2, t1 – времена полураспада веществ В и А). Равновесие, отвечающее этому уравнению, называется вековым. Кроме того, при k 1 << k 2 уравнение для у принимает вид:
y = a (1 –  ).
).
Следовательно, такая реакция протекает как реакция 1-го порядка. Только в самом начале реакции скорость отклоняется от скорости, описываемой уравнением для простой мономолекулярной реакции. Большинство реакций относится к последовательным, в которых конечная стадия протекает значительно быстрее, чем промежуточные.
Для более сложного процесса А ® B ® C ® D добавляется еще одно уравнение для скорости превращения вещества С:
 = k 2 (x – y) – k 3 (y – z),
= k 2 (x – y) – k 3 (y – z),
где (y – z) – число молей вещества С в момент t; z – число молей вещества D.
 + k 3 (y – z) = а
+ k 3 (y – z) = а  (
( –
–  ).
).
После интегрирования
y – z = а (С1  + С2
+ С2  + С3
+ С3  );
);
С1 =  ; С2 =
; С2 = 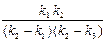 ;
;
С3 =  .
.
Аналогично решается задача при большем количестве звеньев реакции. Для реакций более высокого порядка интегрирование получающихся уравнений не всегда возможно.
Лекция 33
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2832; Нарушение авторских прав?; Мы поможем в написании вашей работы!