
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема про розподіл швидкостей точок тіла
|
|
|
|
Визначимо швидкість т. 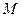 цього тіла. Для цього введемо радіус-вектори
цього тіла. Для цього введемо радіус-вектори  ,
, 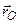 ,
, 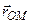 , задаючи таким чином положення т.
, задаючи таким чином положення т. 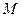 в рухомій і нерухомій системах координат
в рухомій і нерухомій системах координат
(див. рис. 5.4).
 Рис. 5.4.Задання положення т.
Рис. 5.4.Задання положення т. 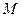 тіла в рухомій і нерухомій системах координат. тіла в рухомій і нерухомій системах координат.
| Розглянемо рух т. 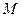 як складний. При цьому поступальний рух разом із полюсом є переносним, а обертальний навколо полюса – відносним. Із рисунка видно, що як складний. При цьому поступальний рух разом із полюсом є переносним, а обертальний навколо полюса – відносним. Із рисунка видно, що
але
(зауважимо, що |
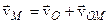 . .
| (5.5) |
Визначимо швидкість 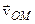 . Оскільки відносний рух – обертальний, то за формулою Ейлера матимемо
. Оскільки відносний рух – обертальний, то за формулою Ейлера матимемо
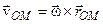 , ,
| (5.6) |
крім цього, враховуючи, що вектор  є завжди перпендикулярним до площини фігури, а вектор
є завжди перпендикулярним до площини фігури, а вектор 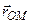 належить цій площині, то
належить цій площині, то
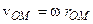 , ,
| (5.7) |
а також
 , ,
| (5.8) |
що завжди виконується.
 Рис. 5.5.До теореми про розподіл швидкостей.
Рис. 5.5.До теореми про розподіл швидкостей.
| Геометричне представлення наведе-них вище формул показано на рис. 5.5. Таким чином, доведена наступна теорема про розподіл швидкостей: швидкість будь-якої точки тіла під час плоскопаралельного руху дорівнює векторній сумі швидкості полюса і швидкості обертального руху навколо полюса. Швидкість обертального руху навколо полюса є завжди перпендикулярною до прямої, що з'єднує точку з полюсом. |
Наслідки:
1) проекції швидкостей двох точок тіла на пряму, що їх з’єднує, є рівними між собою
(рис. 5.6). Це є кінематичне означення абсолютно твердого тіла.
 Рис. 5.6.До наслідку 1.
Рис. 5.6.До наслідку 1.
|
Для доведення виберемо за полюс т.  , тоді , тоді
спроектуємо цю векторну рівність (5.9) на пряму
але
що і треба було довести; |
2) завжди існує точка, незмінно зв’язана (але необов'язково співпадаюча) з твердим тілом, швидкість якої у даний момент часу дорівнює нулю. Ця точка називається миттєвим центром швидкостей (м.ц.ш.).
 Рис. 5.7.До наслідку 2.
Рис. 5.7.До наслідку 2.
| Якщо за полюс вибрати м.ц.ш., то закон розподілення швидкостей у тілі є законом розподілу швидкостей при обертальному русі, тобто тіло виконує миттєве обертання навколо осі, що проходить через м.ц.ш. (див. рис. 5.7). |
5.3. Миттєвий центр швидкостей; способи його знаходження
Розглянемо різні способи побудови м.ц.ш.
1. У твердому тілі відома швидкість  точки
точки  і миттєва кутова швидкість
і миттєва кутова швидкість  (див. рис. 5.8).
(див. рис. 5.8).
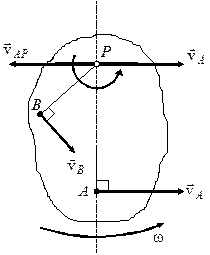 Рис. 5.8.Перший спосіб побудови м.ц.ш.
Рис. 5.8.Перший спосіб побудови м.ц.ш.
| Припустимо, що точка  - м.ц.ш., тобто - м.ц.ш., тобто  . Виберемо за полюс т. . Виберемо за полюс т.  і визначимо швидкість т. і визначимо швидкість т. 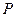 : :
 ,
але ,
але 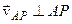 , тоді маємо , тоді маємо 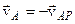 (див. рис. 5.8)
і (див. рис. 5.8)
і  .
Оскільки .
Оскільки  також перпендикулярна до також перпендикулярна до 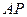 , то м.ц.ш. лежить на прямій, перпендикуляній до , то м.ц.ш. лежить на прямій, перпендикуляній до  . Крім того, . Крім того,  , а отже , а отже  , і тоді , і тоді
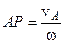 .
Відкладемо відстань .
Відкладемо відстань 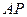 від т. від т.  у напрямі, який визначається знаком у напрямі, який визначається знаком  .
Якщо положення м.ц.ш. знайдено, то швидкість будь-якої точки легко визначити на підставі співвідношення .
Якщо положення м.ц.ш. знайдено, то швидкість будь-якої точки легко визначити на підставі співвідношення
| |
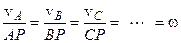 , ,
| (5.10) | |
або
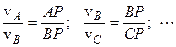 ,
,
тобто швидкості точок плоскої фігури співвідносяться як їх відстані до м.ц.ш.
2. Відомі напрямки швидкостей двох точок тіла (див. рис. 5.9).
 Рис. 5.9.Знаходження м.ц.ш. при довільних напрямках швидкостей.
Рис. 5.9.Знаходження м.ц.ш. при довільних напрямках швидкостей.
|
Тоді, відновлюючи у точках перпендикуляри до напрямків їх швидкостей, отримаємо на перетині цих перпендикулярів шуканий м.ц.ш. 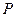 .
Якщо ж напрямки швидкостей двох точок тіла колінеарні, то мають місце наступні частинні випадки, показані на рис. 5.10. .
Якщо ж напрямки швидкостей двох точок тіла колінеарні, то мають місце наступні частинні випадки, показані на рис. 5.10.
|

| 
|
а)  і і  різні і напрямлені в одну сторону різні і напрямлені в одну сторону
| б)  і і  різні і напрямлені в протилежні сторони різні і напрямлені в протилежні сторони
|
| Рис. 5.10.Частинні випадки побудови м.ц.ш. при колінеарних напрямках швидкостей. |
Якщо швидкості двох точок тіла паралельні і рівні (див. рис. 5.11), то тіло виконує миттєво-поступальний рух. Цей рух відрізняється від звичайного поступального тим, що прискорення розглядуваних точок можуть бути й нерівними, навіть якщо швидкості цих точок є рівними

|
| Рис. 5.11. Випадок паралельних і рівних швидкостей. |
3. Положення м.ц.ш. можна визначити і із суто фізичних міркувань (див. рис. 5.12).
 Рис. 5.12. «Фізичний» спосіб визначення положення м.ц.ш.
Рис. 5.12. «Фізичний» спосіб визначення положення м.ц.ш.
| Так у колесі, що котиться без ковзання вздовж горизонтальної прямої, швидкість точки  контакту колеса із землею буде дорівнювати нулю (якщо немає проковзування), тобто ця точка є м.ц.ш. колеса.
Зауважимо, що положення м.ц.ш. (т. контакту колеса із землею буде дорівнювати нулю (якщо немає проковзування), тобто ця точка є м.ц.ш. колеса.
Зауважимо, що положення м.ц.ш. (т. 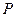 ) змінюється під час руху колеса.
В кожний момент часу м.ц.ш. займає нове положення, геометричне місце м.ц.ш. називається центроїдою, існують рухома і нерухома центроїди (відповідно коло і пряма). ) змінюється під час руху колеса.
В кожний момент часу м.ц.ш. займає нове положення, геометричне місце м.ц.ш. називається центроїдою, існують рухома і нерухома центроїди (відповідно коло і пряма).
|
Теорема Пуансо: будь-який неперервний рух плоскої фігури в її площині можна здійснити коченням без ковзання рухомої центроїди по нерухомій.
(Коченням без ковзання називається рух двох кривих, що мають спільну точку, при якому швидкості спільної точки цих кривих є рівними між собою.)
Зокрема, при плоскопаралельному русі твердого тіла також має місце кочення рухомої центроїди по нерухомій без ковзання.
5.4. План швидкостей
Планом швидкостей називається креслення, на якому графічним методом знаходяться швидкості всіх точок одного тіла або системи твердих тіл, що рухаються у площині.
Знайдемо швидкості всіх точок твердого тіла. Отже, відома (задана) швидкість однієї точки за величиною і напрямком, а також відомий напрямок швидкості іншої точки (див. рис. 5.13).
Треба знайти швидкості всіх точок тіла.
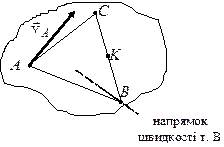 Рис. 5.13.Постановка задачі.
Рис. 5.13.Постановка задачі.
| Виберемо за полюс т.  , тоді , тоді
Рівність (5.11) описує замкнений векторний трикутник, в якому вектор Для цього із довільного полюса |
(рис. 5.13), а з полюса 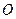 - промінь за напрямком вектора швидкості т.
- промінь за напрямком вектора швидкості т.  . У трикутнику, що утворився:
. У трикутнику, що утворився: 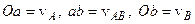 .
.
 Рис. 5.14.План скоростей.
Рис. 5.14.План скоростей.
| Визначимо тепер швидкість довільної т.  . З'єднаємо її з точками . З'єднаємо її з точками  і і  . Виберемо за полюс спочатку т. . Виберемо за полюс спочатку т.  , а потім т. , а потім т.  . Поміщаючи полюс у т. . Поміщаючи полюс у т.  , будемо мати , будемо мати
де
де відомі напрямки Зауважимо, що побудови на плані швидкостей відповідають графічному розв’язанню системи рівнянь (5.12)¸(5.13), тобто побудови |
 , призводять до:
, призводять до: 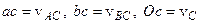 .
.
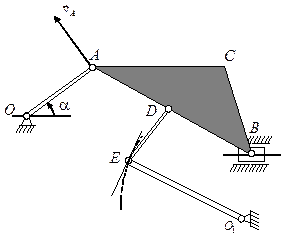
Приклад (побудови плану швидкостей системи твердих тіл).
Для механізму, ланка  якого обертається у додатному напрямку з кутовою швидкістю
якого обертається у додатному напрямку з кутовою швидкістю  , визначити графічно швидкості всіх його точок у положенні, схематично показаному на рис. 5.15.
, визначити графічно швидкості всіх його точок у положенні, схематично показаному на рис. 5.15.
| 
|
| Рис. 5.15.Схема досліджуваного механізму. | Рис. 5.16.План швидкостей для механізму з рис. 5.15. |
Послідовність побудови плану швидкостей така (див. рис. 5.16):
1) обчислюємо швидкість т.  і будуємо вектор
і будуємо вектор  у масштабі від довільно вибраного полюса
у масштабі від довільно вибраного полюса  на плані швидкостей (
на плані швидкостей ( );
);
2) визначаємо швидкість т.  (оскільки відомий її напрямок), користуючись формулою:
(оскільки відомий її напрямок), користуючись формулою:
 ,
,
для чого через т. 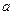 на плані швидкостей проводимо пряму
на плані швидкостей проводимо пряму  , перпендикулярну до відрізку
, перпендикулярну до відрізку  , до перетину в т.
, до перетину в т.  із відомим напрямком швидкості т.
із відомим напрямком швидкості т.  , проведеним із полюса
, проведеним із полюса 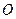 ; тоді
; тоді 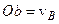 ;
;
3) для знаходження швидкості т.  розв'язуємо графічно систему рівнянь
розв'язуємо графічно систему рівнянь

в цьому випадку т.  на плані швидкостей знаходиться як перетин перпендикулярів до сторін
на плані швидкостей знаходиться як перетин перпендикулярів до сторін  і
і  вихідного
вихідного 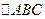 (тобто
(тобто 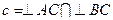 ), і крім цього
), і крім цього 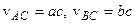 ; отже,
; отже,  ;
;
4) швидкість т. 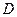 визначається із урахуванням того, що ця точка ділить сторону
визначається із урахуванням того, що ця точка ділить сторону  і відрізок
і відрізок  плану в однаковому відношенні (оскільки побудови проводилися в одному масштабі), тобто
плану в однаковому відношенні (оскільки побудови проводилися в одному масштабі), тобто
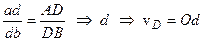 .
.
5) знайдемо тепер швидкість т. 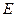 . Врахувавши те, що
. Врахувавши те, що  , проводимо
, проводимо  і з т.
і з т. 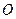 пряму, що має напрямок швидкості
пряму, що має напрямок швидкості 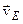 ; отримуємо у перетині точку
; отримуємо у перетині точку  , тоді
, тоді 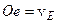 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1557; Нарушение авторских прав?; Мы поможем в написании вашей работы!
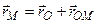 ,
,
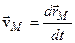 , тоді, здиференціювавши рівність (5.4), отримаємо
, тоді, здиференціювавши рівність (5.4), отримаємо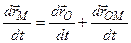 або
або 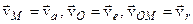 ), де
), де  ,
,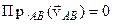 (оскільки
(оскільки  ), тому
), тому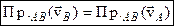 ,
, відомі за напрямком:
відомі за напрямком:  . Побудуємо цей трикутник.
. Побудуємо цей трикутник.
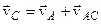 ,
,
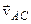 - за напрямком (
- за напрямком ( ). Якщо ж розташувати полюс у
). Якщо ж розташувати полюс у 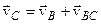 ,
,
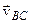 (
(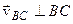 ).
).