Лекция №2. 1. Схемы замещения электрических цепей

План лекции:

1. Схемы замещения электрических цепей

2. Эквивалентные преобразования пассивных электрических цепей

3. Расчет цепей посредством двух законов Кирхгофа

4. Мощность в цепях постоянного тока

5. Баланс мощностей

1. Схемы замещения электрических цепей

Схемой электрической цепи называется ее графическое изображение с использованием обозначений идеальных элементов. Например:

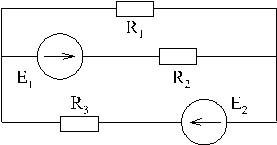
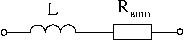
Если учесть сопротивление утечки реального конденсатора, сопротивление витков реальной индуктивной катушки и внутреннее сопротивление реального источника ЭДС, то можно составить соответствующие схемы замещения этих элементов:

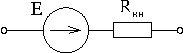
Отсюда следует, что все схемы по сути дела являются лишь более или менее точными схемами замещения реальных электрических цепей.

Представленный на рис.2 контур содержит три участка: участок с постоянным напряжением U = Е, не зависящим от тока источника, и участки с напряжениями RвхI и U на нагрузке Rн.

Направление ЭДС выбрано совпадающим с направлением тока, но оно противоположно напряжению на этом элементе.

Для определения параметров схемы замещения источника электрической энергии с линейной внешней характеристикой нужно провести два опыта - холостого хода (I=0; U=Uх=Е) и короткого замыкания (I=Iк; U=Е-RвнI).

2. Эквивалентные преобразования пассивных электрических цепей

Для упрощения анализа сложных электрических цепей отдельные их участки, не содержащие ЭДС, или пассивные цепи целиком можно заменить одним эквивалентным сопротивлением. Под эквивалентным понимают такое сопротивление, которое, будучи включенным в цепь вместо заменяемой группы сопротивлений, не изменяет распределение токов и напряжений в остальной части цепи.

При последовательном соединении сопротивлений по каждому из них

протекает один тот же ток, следовательно, падение напряжения на эквивалентном сопротивлении должно быть равно сумме падений напряжений на исходных сопротивлениях:

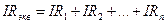
отсюда получаем:

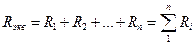
Если группа заменяемых сопротивлений соединена параллельно, то

напряжения на каждом из них и на эквивалентном сопротивлении одинаковы. Условия эквивалентности будут выполнены, если ток через искомое сопротивление будет равен сумме токов через отдельные параллельные сопротивления:

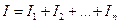
Используя закон Ома для отдельного сопротивления, можем записать:

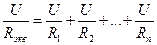
Окончательно получаем:

Поскольку величина, обратная сопротивлению, есть проводимость, то, вводя обозначения для проводимости 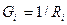, получим:

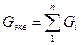
При анализе сложных схем встречаются случаи, когда часть схемы образует так называемый треугольник сопротивлений:

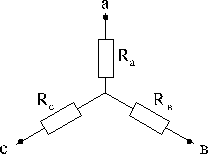
Схема упрощается, если треугольник с сопротивлениями Rав, Rвс, Rса заменить эквивалентной звездой с сопротивлениями Rа, Rв, Rс. Иногда, наоборот, необходимо обратное преобразование звезды в треугольник. Схемы треугольника и звезды считаются эквивалентными, если после преобразования все токи и напряжения в остальных частях схемы (не затронутых преобразованиями) остаются неизменными.

Очевидно, условия эквивалентности должны выполняться и при обрыве проводов, подходящих к узлам "а", "в", "с". Например, при обрыве провода, подходящего к узлу "а", сопротивления между точками "в" и "с" в треугольнике и звезде должны быть одинаковы, т.е.:

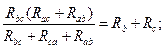
Рассуждая аналогичным образом, можно записать:

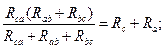
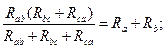
Решая полученную систему уравнений относительно Rа, Rв и Rс, получим формулы эквивалентного преобразования треугольника в звезду:

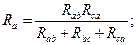
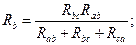
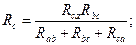
Решая систему относительно 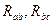и 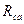получим формулы преобразования звезды в треугольник:

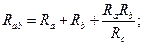
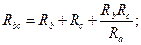
В частном случае, когда сопротивления звезды или треугольника одинаковы, эти формулы упрощаются:

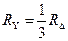
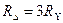
3. Расчет цепей посредством двух законов Кирхгофа

Порядок расчета:

а) произвольно задаются положительными направлениями токов во всех ветвях схемы,

б) для всех узлов схемы кроме одного составляются уравнения по 1-му закону Кирхгофа,

в) для всех независимых контуров составляются уравнения по 2-му закону Кирхгофа (контур будет считаться независимым от остальных, если в него входит хотя бы одна новая ветвь, т.е. не вошедшая в состав других контуров).

Общее число уравнений, составленных по 1 и 2-му законам Кирхгофа должно быть равно числу неизвестных токов. Полученная система линейных уравнений разрешается относительно токов с использованием известных методов решения систем уравнений (например, с помощью определителей)

Пример:

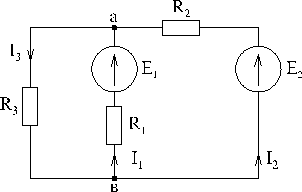
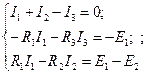
Если при решении системы уравнений значение какого-либо тока получилось отрицательным, то это означает, что истинное направление тока противоположно выбранному. Данный метод расчета является универсальным, однако расчет вручную возможен лишь для несложных схем (4-5 неизвестных тока). Для более сложных схем требуется применение иных методов или вычислительной техники.

4. Мощность в цепях постоянного тока

Для оценки энергетических условий важно знать сколь быстро совершается работа.

Отношение работы "А" к соответствующему промежутку времени t определяет мощность: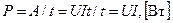

Используя закон Ома, можно получить другие формулы для мощности в электрических цепях:

5. Баланс мощностей

В любой электрической цепи должен соблюдаться энергетический баланс - баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

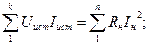
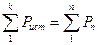
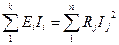
В левой части равенства слагаемое берется со знаком "+" если Е и I совпадают по направлению и со знаком "-" если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

Например:

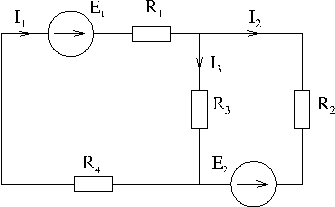
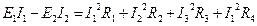
Дата добавления: 2014-01-07