Лекция 1. Понятие функции комплексного переменного. Предел и непрерывность функции комплексного переменного. Дифференцирование функции. Условие Коши-Римана

Областью на комплексной плоскости С называется множество точек, удовлетворяющее двум условиям:

а) Условие открытости: если 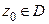, то множество 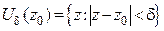также содержится в ;

б) Свойство связности: любые две точки из можно соединить ломаной, состоящей из точек .

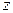Граница области – это множество точек , каждая из которых области не принадлежит, но в любой 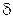-окрестности 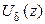содержатся точки не . Область вместе со своей границей называют замкнутой областью.

Определение 1. Если каждому комплексному числу 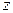из области поставлено в соответствие некоторое комплексное число 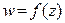, то говорят в области задана функция комплексного переменного.

Так как всякое комплексное число 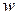можно представить в алгебраической форме в виде , то запись в виде , где 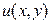– действительная и – мнимая части – называется алгебраической формой функции комплексного переменного.

Определение 2. Пусть функция 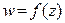определена в некоторой окрестности точки 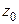, кроме, быть может, самой точки 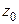. Число 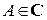называется пределом функции в точке 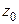, если для , что для всех 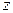, удовлетворяющих условию , имеет место неравенство .

В этом случае используют формальную запись

. (1)

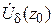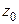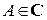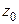Теорема 1. Пусть функция определена в некоторой «проколотой» окрестности точки . Для того, чтобы число было пределом в точке , необходимо и достаточно, чтобы существовали два предела:

где .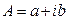

Отметим, что как и в действительном анализе, справедливым является следующее утверждение: для того, чтобы существовал предел (1) необходимо и достаточно, чтобы для любой последовательности соответствующая последовательность .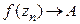

Определение 2. Пусть функция 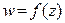определена в некоторой окрестности точки 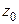. Она называется непрерывной в точке 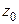, если существует предел в точке 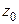и он равен 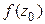, т.е.

. (2)

Несложным следствием из теоремы 1 является следующая

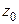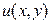Теорема 2. Для того, чтобы функция , определенная в некоторой окрестности точки , была непрерывна в этой точке, необходимо и достаточно, чтобы в точке , где , были непрерывны функции и .

Функция 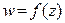, определенная в некоторой области , называется непрерывной в , если она непрерывна в любой точке этой области.

На непрерывные функции комплексного переменного естественным образом переносятся все теоремы о непрерывных функциях действительного переменного.

Определение 3. Будем говорить, что функция 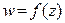, определенная в некоторой окрестности точки 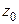дифференцируема в этой точке, если существует предел

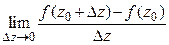. (3)

Сам этот предел называется производной функции в точке .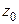

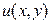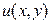По аналогии с непрерывностью функции комплексного переменного хотелось бы сформулировать и доказать утверждение о достаточности дифференцируемости двух функций двух действительных переменных и в точке для дифференцируемости в точке функции . На самом деле, это не так. Дифференцируемость в точке накладывает важные дополнительные условия связи функций и , называемые условиями Коши-Римана (-Даламбера-Эйлера).

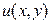Теорема 3. Пусть функция определена в некоторой окрестности точки и функции и дифференцируемы в точке . Тогда для дифференцируемости функции в точке 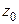необходимо и достаточно, чтобы в точке имели место соотношения:

, ,

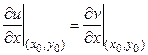называемое условиями Коши-Римана.

Из определения производной функции 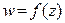непосредственно следует, что обычные правила дифференцирования функций сохраняются.

Дата добавления: 2014-01-07