
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упражнения
|
|
|
|
1. Доказать, что для 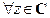 и
и 
 -окрестность точки
-окрестность точки  является областью. Определить
является областью. Определить  .
.
2. Записать в виде неравенства область  .
.
3. Пусть  – кольцо с центром в точке
– кольцо с центром в точке 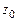 . Является ли оно областью?
. Является ли оно областью?
4. Следующие функции комплексного переменного записать в алгебраической форме:
а) Линейная:  б)
б) 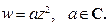
5. Записать на языке 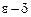 :
:
а)  ; б)
; б)  ; в)
; в)  .
.
6. Доказать теорему 1. Указание: воспользоваться равенством  и неравенством
и неравенством 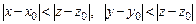 .
.
7. Пусть  и
и  . Показать, что тогда последовательность
. Показать, что тогда последовательность 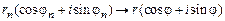 .
.
8. Доказать, что для 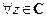
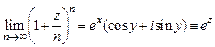 .
.
9. Доказать теорему 2.
10. Доказать необходимость условий Коши-Римана в теореме 3. Указание: существование предела (3) не зависит от способа стремления 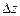 к нулю. Получить явное выражение для этого предела, когда
к нулю. Получить явное выражение для этого предела, когда  , и вывести из полученных выражений условия Коши-Римана.
, и вывести из полученных выражений условия Коши-Римана.
11. Доказать достаточность условий Коши-Римана в теореме 3. Указание: используя выражения приращений  и
и 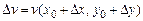 через полные дифференциалы, записать приращение
через полные дифференциалы, записать приращение 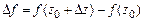 в виде
в виде
 ,
,
где  и
и 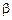 – бесконечно малые относительно
– бесконечно малые относительно  функции. Далее воспользоваться условиями Коши-Римана при вычислении предела (3).
функции. Далее воспользоваться условиями Коши-Римана при вычислении предела (3).
12. Доказать, что производная  может быть вычислена по следующим формулам:
может быть вычислена по следующим формулам:
 .
.
13. Доказать, что в любой точке  функция
функция  (определение см. в упражнении 8) дифференцируема и
(определение см. в упражнении 8) дифференцируема и  .
.
Лекция 2. Аналитические функции и их свойства. Интеграл функции комплексного переменного. Интегральная теорема Коши.
Неопределенный интеграл. Формула Коши. Интеграл типа Коши.
Определение 4. Функция  , определенная в некоторой области
, определенная в некоторой области  и имеющая в этой области непрерывную производную
и имеющая в этой области непрерывную производную  , называется аналитической в области
, называется аналитической в области  .
.
Теорема 3, по существу, утверждает, что необходимым и достаточным условием аналитичности функции является существование и непрерывность в  частных производных
частных производных 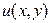 и
и  , связанных условиями Коши-Римана.
, связанных условиями Коши-Римана.
Верны следующие свойства аналитических в  функций:
функций:
1°. Сумма, разность, произведение и частное (если знаменатель отличен от нуля) аналитических в  функций есть функция аналитическая.
функций есть функция аналитическая.
2°. Суперпозиция аналитических функций является аналитической функцией.
3°. Если в области определена аналитическая функция  , причем
, причем  и
и  – область, то в существует аналитическая функция,
– область, то в существует аналитическая функция, 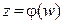 , отображающая
, отображающая  на
на  и являющаяся обратной к
и являющаяся обратной к  , т.е.
, т.е.  и
и 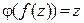 . При этом
. При этом 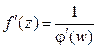 .
.
4°. Пусть в области  плоскости
плоскости 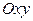 задана функция
задана функция 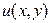 , являющаяся действительной частью аналитической функции. Тогда мнимая часть этой функции
, являющаяся действительной частью аналитической функции. Тогда мнимая часть этой функции  определяется с точностью до константы.
определяется с точностью до константы.
Пусть на комплексной плоскости С задана кусочно-гладкая кривая  , определяемая параметрическими уравнениями
, определяемая параметрическими уравнениями  , где
, где  и
и  – кусочно-гладкие функции действительного параметра
– кусочно-гладкие функции действительного параметра  . Пусть точки
. Пусть точки 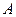 и
и  являются концами кривой
являются концами кривой  . При изменении параметра
. При изменении параметра  от
от 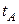 к
к 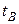 точка
точка 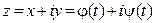 перемещается по кривой
перемещается по кривой  . Пусть далее
. Пусть далее 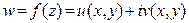 – функция комплексного переменного, непрерывная на кривой
– функция комплексного переменного, непрерывная на кривой  . Разобьем кривую
. Разобьем кривую  на n частичных дуг точками
на n частичных дуг точками  и определим сумму
и определим сумму
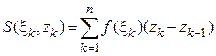 , (4)
, (4)
где 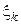 – произвольная точка частичной дуги, лежащая между точками
– произвольная точка частичной дуги, лежащая между точками 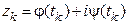 и
и  .
.
Определение 5. Если при  , где
, где  , существует предел сумм (4), не зависящий ни от способа разбиения кривой
, существует предел сумм (4), не зависящий ни от способа разбиения кривой  точками
точками  на частичные дуги, ни от выбора точек
на частичные дуги, ни от выбора точек 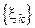 , то этот предел называется интегралом от функции
, то этот предел называется интегралом от функции  по кривой
по кривой  , т.е.
, т.е.
 . (5)
. (5)
Свойства интеграла (5):
1°.  ;
;
2°. 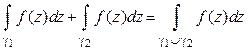 (аддитивность);
(аддитивность);
3°. 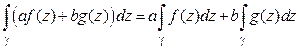 (линейность);
(линейность);
4°.  ;
;
5°.  , где
, где  – аналитическая функция, устанавливающая взаимнооднозначное соответствие между
– аналитическая функция, устанавливающая взаимнооднозначное соответствие между  и
и 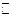 . В частности,
. В частности,
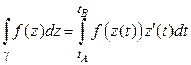 (6)
(6)
6°. 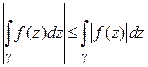 .
.
Формула (6) при удачно выбранном способе параметризации кривой  используется для вычисления интеграла (5) функции
используется для вычисления интеграла (5) функции  по кривой
по кривой  .
.
Теорема 4 (Коши). Пусть в односвязной области D задана однозначная аналитическая функция  . Тогда интеграл по любому замкнутому контуру
. Тогда интеграл по любому замкнутому контуру  , целиком лежащему в этой области, от функции
, целиком лежащему в этой области, от функции  равен нулю, т.е.
равен нулю, т.е.
 . (7)
. (7)
Теорема 5. Если функция  является аналитической в односвязной области D, ограниченной кусочно-гладким контуром
является аналитической в односвязной области D, ограниченной кусочно-гладким контуром  , и непрерывна в
, и непрерывна в 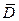 , то верна формула (7).
, то верна формула (7).
Теорема 5 Коши допускает обобщение и на многосвязные области. Действительно, верна
Теорема 6. Пусть  однозначная аналитическая функция в многосвязной области D, непрерывная в
однозначная аналитическая функция в многосвязной области D, непрерывная в 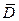 и D ограничена извне кусочно-гладким контуром
и D ограничена извне кусочно-гладким контуром  , а изнутри кусочно-гладкими контурами
, а изнутри кусочно-гладкими контурами  . Тогда
. Тогда
 .
.
Пусть  – однозначная аналитическая функция, заданная в односвязной области D. Фиксируем некоторую точку
– однозначная аналитическая функция, заданная в односвязной области D. Фиксируем некоторую точку 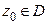 и рассмотрим интеграл
и рассмотрим интеграл
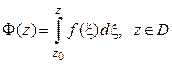 , (8)
, (8)
зависящий только от точки z, и не зависящий от пути интегрирования (см. упр. 24).
Теорема 7. Пусть функция  аналитична в D. Тогда функция
аналитична в D. Тогда функция  , определенная формулой (8), также аналитическая в D и
, определенная формулой (8), также аналитическая в D и  для
для  .
.
Определение 6. Функция  , определенная формулой (8), называется неопределенным интегралом аналитической в области D функции
, определенная формулой (8), называется неопределенным интегралом аналитической в области D функции  .
.
Теорема 8 (формула Коши). Пусть функция  аналитична в односвязной области D и
аналитична в односвязной области D и  -замкнутый, кусочно-гладкий контур без самопересечений, целиком лежащий в D. Тогда для любой точки
-замкнутый, кусочно-гладкий контур без самопересечений, целиком лежащий в D. Тогда для любой точки 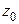 , лежащей внутри контура
, лежащей внутри контура  , верна следующая формула Коши:
, верна следующая формула Коши:
 . (9)
. (9)
Существует обобщение формулы Коши (9), которое называется формулой типа Коши. Сформулируем это утверждение без доказательства:
Пусть функция  аналитична в D и непрерывна в
аналитична в D и непрерывна в 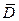 . Тогда в области D у нее существует непрерывная производная любого порядка n, которая может быть вычислена в любой точке
. Тогда в области D у нее существует непрерывная производная любого порядка n, которая может быть вычислена в любой точке 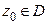 по формуле:
по формуле:
 . (10)
. (10)
Упражнения.
14. Доказать свойства аналитических функций 1º– 4º. Указание. Доказательство свойства 3º получается с помощью следующих рассуждений. Пусть 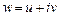 . Тогда функции
. Тогда функции  и
и  задают отображение области
задают отображение области 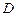 двумерной плоскости
двумерной плоскости  на область
на область  плоскости
плоскости 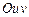 . Это отображение невырождено, т.к. его якобиан
. Это отображение невырождено, т.к. его якобиан  (Проверить, используя условия Коши-Римана!). По теореме об обратном отображении функции
(Проверить, используя условия Коши-Римана!). По теореме об обратном отображении функции  и
и  однозначно отображают
однозначно отображают 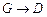 . Наконец, полагаем
. Наконец, полагаем  . Для доказательства свойства 4º заметим, что
. Для доказательства свойства 4º заметим, что
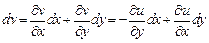
и  восстанавливается с точностью до константы с помощью криволинейного интеграла 2-го рода.
восстанавливается с точностью до константы с помощью криволинейного интеграла 2-го рода.
15. Определить области аналитичности следующих функций комплексного переменного:
а) Многочлен  ;
;
б) Тригонометрические:  ;
;
в) Гиперболические: 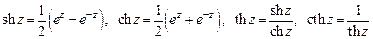 .
.
16. Проверить тождества:

17. Доказать свойства 1º-6º интеграла (5). Указание. Везде использовать соответствующее преобразование интегральных сумм (4).
18. Доказать эквивалентность утверждения, сформулированного в свойстве 4º, и определения 5 интеграла 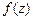 по кривой
по кривой 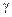 .
.
19. Вычислить  , где
, где 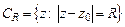 и n – произвольное целое число.
и n – произвольное целое число.
20. Доказать теорему 4 (Коши). Указание. Воспользоваться свойством 4, приманить к каждому из полученных интегралов формулу Грина, а затем воспользоваться условиями Коши-Римана.
21. Доказать теорему 5. Указание. Точками  разбить контур
разбить контур 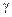 на частичные дуги. Соединить эти точки отрезками и доказать, что интегралы функции
на частичные дуги. Соединить эти точки отрезками и доказать, что интегралы функции 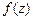 по замкнутой ломаной
по замкнутой ломаной 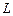 ,образованной этими отрезками, и контуру
,образованной этими отрезками, и контуру 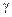 мало отличаются.
мало отличаются.
22. Пусть 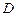 – односвязная область площади
– односвязная область площади 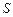 , ограниченная кусочно-гладким контуром
, ограниченная кусочно-гладким контуром 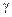 . Доказать равенства:
. Доказать равенства:
а) 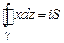 ;
;
б)  ;
;
в) 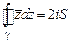 .
.
23. Доказать теорему 6. Указание. Соединить внутренние контуры 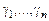 разрезами с внешним контуром
разрезами с внешним контуром  , превратив область
, превратив область 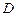 в односвязную. Применить теорему Коши к полученному сложному контуру и учесть, что отрезки разрезов при вычислении интеграла проходятся дважды.
в односвязную. Применить теорему Коши к полученному сложному контуру и учесть, что отрезки разрезов при вычислении интеграла проходятся дважды.
24. Доказать утверждение: если 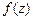 однозначная аналитическая функция в области
однозначная аналитическая функция в области 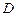 и
и 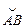 – кусочно-гладкая душа без самопересечений, целиком содержащаяся в
– кусочно-гладкая душа без самопересечений, целиком содержащаяся в 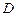 , то интеграл по дуге
, то интеграл по дуге 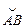 от функции
от функции 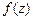 не зависит от вида дуги, а только от взаиморасположения точек
не зависит от вида дуги, а только от взаиморасположения точек  и
и  .
.
25. Доказать теорему 7. Указание. Показать, что верно неравенство
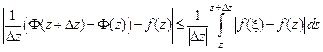 ,
,
так что для 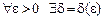 такое, что, если
такое, что, если  , то
, то
 .
.
26. Доказать, что все аналитические функции, являющиеся неопределенными интегралами аналитической функции  , отличаются на константу.
, отличаются на константу.
27. Доказать формулу Ньютона-Лейбница:
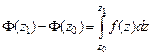 ,
,
связывающую понятия определенного и неопределенного интегралов для аналитических функций комплексного переменного.
28. Доказать формулу Коши (теорема 8). Указание. Пусть 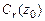 – окружность радиуса
– окружность радиуса 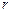 с центром в точке
с центром в точке 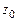 , целиком лежащая внутри контура
, целиком лежащая внутри контура 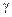 . Показать, что
. Показать, что
 .
.
Далее доказать, что для  такое, что верна оценка
такое, что верна оценка
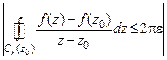 .
.
29. Доказать, что в условиях формулы Коши, если 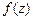 дополнительно непрерывна вплоть до границы
дополнительно непрерывна вплоть до границы 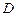 , то в формуле (9) за контур
, то в формуле (9) за контур 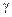 можно принять границу
можно принять границу 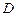 .
.
30. Доказать следующую формулу среднего значения аналитической функции 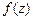 :
:
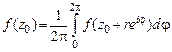 .
.
Указание: Выбрать за контур 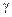 окружность
окружность 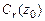 .
.
31. Доказать следующую теорему Морера: пусть 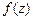 непрерывна в односвязной области
непрерывна в односвязной области 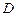 и интеграл от нее по любому замкнутому контуру, целиком лежащему в
и интеграл от нее по любому замкнутому контуру, целиком лежащему в 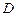 , равен нулю. Тогда
, равен нулю. Тогда 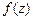 – аналитическая в
– аналитическая в 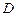 . Указание. Показать, что утверждение теоремы 7 остается справедливым, если условие аналитичности
. Указание. Показать, что утверждение теоремы 7 остается справедливым, если условие аналитичности 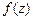 заменить на ее непрерывность и равенство нулю интеграла по любому замкнутому контуру.
заменить на ее непрерывность и равенство нулю интеграла по любому замкнутому контуру.
32. Доказать следующую теорему Лиувилля: пусть 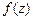 – аналитическая по всей комплексной плоскости и
– аналитическая по всей комплексной плоскости и  для
для 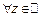 . Тогда
. Тогда  . Указание. Воспользоваться формулой типа Коши для 1-ой производной.
. Указание. Воспользоваться формулой типа Коши для 1-ой производной.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 372; Нарушение авторских прав?; Мы поможем в написании вашей работы!