Теорема разложения

Любую функцию 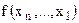можно разложить по переменной 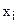в форме

.

Теорема легко доказывается методом перебора значений переменной :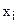

1)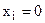подставляем в левую и правую части равенства

и получаем тождество;

2)подставляем в левую и правую части равенства

также получаем тождество. Следовательно, при всех возможных значениях 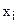исходное равенство справедливо.

По принципу двойственности исходное равенство можно записать в другой форме, заменив нули единицами, единицы нулями, операции дизъюнкции – конъюнкциями, а конъюнкции – дизъюнкциями.

.

С теоремой разложения связаны два тождества:

,

.

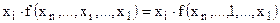Доказывается умножением формулы разложения на 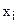и .

Приведенный набор элементарных операций И, ИЛИ, НЕ образует функционально полную систему булевых функций, через которые можно выразить все остальные. Помимо перечисленных основных функций используется ряд других. Все функции можно представить в виде таблицы.

x1					Наименование операции	Обозначение
x2
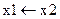
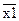
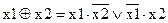
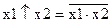
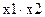
F0 F1 F2   F3 F4 F5 F6 F7 F8 F9 F10   F11 F12 F13 F14 F15					Константа 0 Инверсия суммы или стрелка Пирса Запрет по х2   Инверсия х2 Запрет по х1 Инверсия х1 Исключающее ИЛИ, неравнозначность Инверсия И или штрих Шеффера Конъюнкция Равнозначность х1   Импликация х1 х2 Импликация х2 Дизъюнкция Константа 1	х1 х2

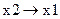
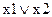
Импликация х1 – если х1 истинно, то оно следует из любого высказывания х2, если ложно – то из него следует любое х2.

Дата добавления: 2014-01-07