Система обыкновенных дифференциальных уравнений луча в виде удобном для численного интегрирования

Уравнение поля времен есть уравнение кривой, определяющей положение волнового фронт в заданный момент времени. По мере возрастания времени волновой фронт перемещается в новое положение. Лучи остаются фиксированными в пространстве. В настоящем случае нас интересует их положение для заданного источника и среды с заданной скоростью v(x,z). Величину t (время) полезно использовать в качестве параметра для задания уравнений

x=x(t), z=z(t), θ=θ(t), (3.1)

которые представляют собой параметрические уравнения некоторого луча, где t означает время пробега по этому лучу от некоторой начальной точки. Из определения луча (верного только для изотропной среды) как нормали к волновому фронту следует, что вектор, направленный вдоль луча, есть

(3.2)

Его называют вектором медленности

(3.3)

Выведем формулу уравнения луча для среды v=v(x,z)

рис. 3.1.

Направляющие косинусы луча, вышедшего из источника (x_0,z₀), будут

, (3.4)

где θ – переменный угол наклона луча к оси х, ds - элемент дуги по лучу (рис.3.1).

Введем t - текущее переменное время – параметр луча.

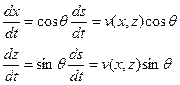, (3.5)

где ds/dt=v(x,z) -скорость распространения волн. С другой стороны, направляющие косинусы луча получаются при делении левой и правой частей уравнения поля времен на величину обратную квадрату скорости (рис. 3.2).

	рис. 3.2.

(3.6)

Обозначим 1/v(x,z)=n(x,z). Перенося n(x,z) в левую часть уравнений и дифференцируя верхнее равенство по z, а нижнее по x, получим следующее

, (3.7)

так как

. (3.8)

Далее

. (3.9)

Преобразуем далее это уравнение, учитывая (3.9)

(3.10)

Таким образом, в двухмерном случае сейсмический луч описывается системой трех простых дифференциальных уравнений первого порядка.

,

, (3.11)

.

Решить эту систему уравнений можно численными методами. Если задана функция скорости или скорость задана таблично (в узлах некоторой сетки), необходимо также задать начальные условия: точку (x_0, z₀), через которую проходит луч, и направление луча в этой точке – θ ₀ начальный угол, а также величину шага интегрирования.

В результате получим для заданных значений t значения x(t), z(t), θ(t) для искомых точек луча

Дата добавления: 2014-01-07