Интерполяция годографов в двухмерно-неоднородной среде

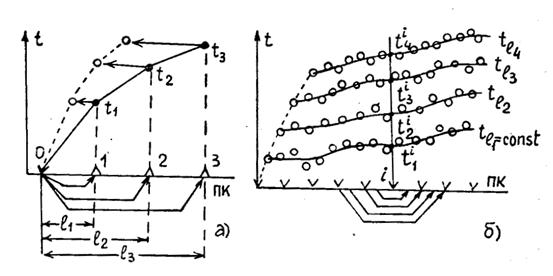Рис.3.6

Сейсмические годографы вдоль профиля описываются функцией 2-х переменных t(x₀, x), где x -координата приемника, x₀ - координата источника. Эта функция всегда задана дискретно.

Интерполяция используется, когда необходимо вычислить какие-либо производные. Без этого любые сейсмические построения невозможны. Линейная интерполяция вносит наименьшие искажения в интерполируемые годографы. Чтобы построить двухмерный разрез, нужна двухмерная интерполяция годографов. Для интерполяции используется разрез офсетов или разрез равных удалений источник приемник.

Разрез офсетов является наблюденным временным полем, это годографы, преобразованные к следующим координатам.

.

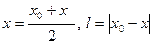Здесь x -середина расстояния источник-приемник, l -офсет (расстояние источник-приемник).

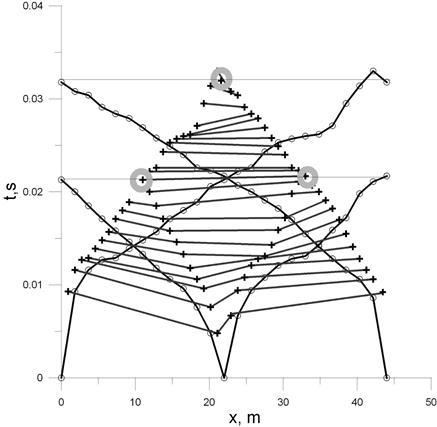
Чтобы построить разрез постоянных офсетов, мы начинаем с равномерной линейной интерполяции каждого годографа (с постоянным интервалом) между приемниками, расстояния при этом отсчитываются от источника (рис. 17, 18). Следующий шаг состоит в отнесении каждого интерполированного значения к середине расстояния источник-приемник (рис.17). Взаимные точки в результате оказываются представленными одной точкой (Рис.19). Времена, соответствующие равным офсетам, мы соединяем прямой линией. Полученное в результате временное поле есть поле изолиний офсетов. Такое поле однозначно и непрерывно. Его легко интерполировать, то есть вычислить годограф с источником в любой точке профиля, как это показано на рисунках 20 и 21, где представлен разрез равных офсетов по профилю на берегу Печорского моря.

рис. 3.7.

		Рис. 3.8.
	Рис. 3.9

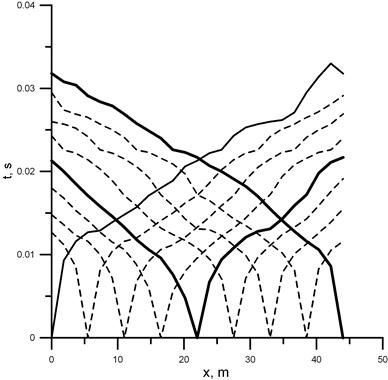
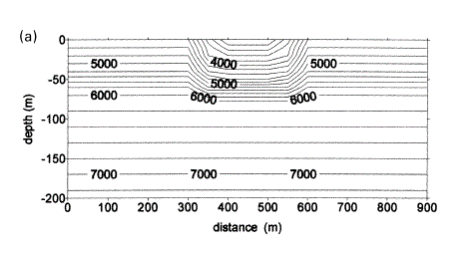
Рис. 3.10.

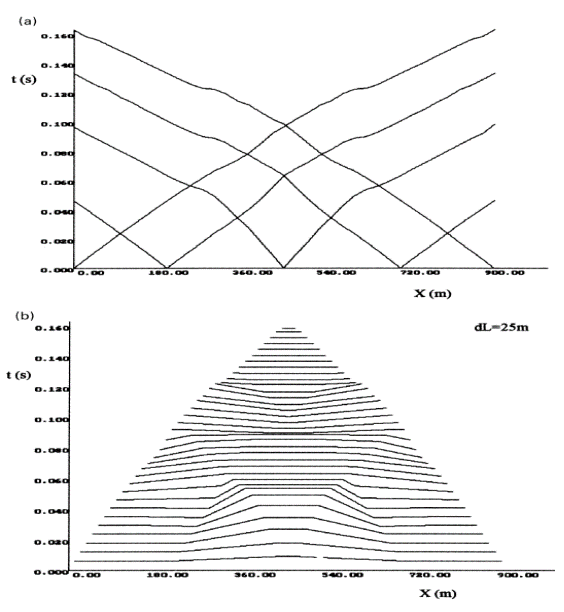Рис. 3.11.

Чтобы построить более детальный разрез можно использовать интерполяцию. Если система годографов достаточно полная и равномерная, нет необходимости использовать интерполяцию Алгоритм интерполяции предложен Пузыревым Н,Н, в 1963 г. Линейная равномерная интерполяция является сглаживающей процедурой. Даже для самых длинных расстояний между источниками, лучи двух встречных годографов пронизывают общий объем разреза внутри луча, который соединяет источники. Следовательно, между двумя встречными годографами всегда может быть произведена интерполяция

Из рис. 19 мы видим, что расстояние между изолиниями офсетов изменяется с изменением наклона годографов. Таким образом, мы можем видеть смену волн или смену слоев на временном разрезе. Главные особенности глубинного разреза отображаются на временном разрезе офсетов. На рис 22 изображена модель с провалом в верхнем слое. На разрезе офсетов (рис 22 внизу) четко отображается структура разреза. Визуальное сравнение окончательного глубинного и наблюденного временного разрезов позволяет нам сделать заключение о том, правильны ли наши глубинные построения.

Дата добавления: 2014-01-07