Элементы теории подобия

Модель среды с однородной функцией скорости.

Для вертикально-неоднородной среды все годографы на поверхности среды идентичны друг другу, и для решения обратной задачи - восстановления зависимости скорости от глубины - достаточно задать годограф из одного любого источника. Для восстановления произвольной скоростной функции двух координат необходима полная система годографов на поверхности среды, когда источники и приёмники заданы с постоянным одинаковым шагом по профилю.

Ясно, что в случае произвольной скоростной функции двух координат, годографы из двух соседних источников могут произвольным образом отличаться друг от друга. Однако, геологические среды, как правило, слоисты и годографы рефрагированных волн, зарегистрированные в двух соседних точках профиля, обладают всегда некоторым сходством, похожи друг на друга. Мерой сходства может быть подобие.

Предположим, что скоростная функция такова, что годографы на поверхности среды подобны друг другу.

Покажем, что такими свойствами обладают среды, где скорость сейсмических волн - однородная функция двух координат.

Подобные явления (физические поля, геометрические фигуры) - это такие явления, которые могут быть совмещены после линейного преобразования переменных, описывающих эти явления.

Пусть каждое из подобных явлений описывается n переменными: (х 1, х 2 ,..., хi,..., xn), где i - номер переменной, N - количество явлений и a - параметр, номер явления, так что 1 < a < N. Явления, подобные между собой, являются подобными, если одноимённые переменные этих явлений связаны между собой линейными соотношениями:

{{ x_ia = C_ia x_{i 1}} ⁿ _{i= 1}} ^N_{a= 1};

Данные равенства описывают преобразования подобия.Известно также, что дифференциальные или алгебраические уравнения, характеризующие подобные явления, остаются инвариантными относительно преобразований подобния.

4.2. Исследование уравнения поля времён в неоднородной среде методами теории подобия.

Рассмотрим уравнение поля времён в неоднородной среде, где скорость волн — произвольная функция двух координат v = v (x,z).

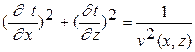(4.1)

Начальное условие t (x 0, z 0 ) = 0 задаёт точку источника.

Введём линейное преобразование переменных:

х = С ₁ х _1,

z = C ₂ z _1,

t = C ₃ t _1. (4.2)

Посмотрим, при каких соотношениях констант С ₁, С ₂, С ₃ и ограничениях на функцию v (x, z) уравнение поля времён остаётся инвариантным относительно преобразований (13):

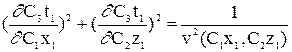(4.3)

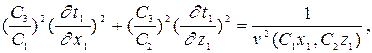(4.4)

Пусть С ₁ = С ₂ и v (x,z) такова, что выполняется равенство

v (C ₁ x ₁, C ₁ z ₁ ) = C ₁ ^m v (x ₁, z ₁ ). (4.5)

Тогда

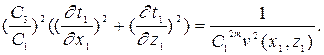(4.6)

При условии

(С ₃ / С ₁ )² = 1 / (С ₁) ^{2 m,} ,

С ₃ = С ₁^{1 - m}, (4.7)

уравнение поля времён (12) остаётся инвариантным относительно линейных преобразований (13):

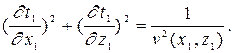(4.8)

Уравнение (4.6) после преобразований (4.5) при условии (4.7) остается неизменным, следовательно, поля времён, описываемые этим уравнением и введенными преобразованиями, подобны.

Условие v (C ₁ x ₁ ,C ₁ z ₁ ) = C ₁ ^m v (x ₁, z ₁ ) выделяет класс однородных функций.

По определению, однородная функция f = f (x,y) удовлетворяет равенству

f (Cx, Cy) = C^m f (x, y),

где m - степень однородной функции, действительное число, - ∞ < m < + ∞. Однородную функцию в декартовых координатах нельзя описать определённой формулой. В полярной системе координат однородные функции имеют более конкретную формулу.

Дата добавления: 2014-01-07