Уравнение фронта волны и параметрa луча

Вывод уравнения фронта волны для сред, где скорость волн - однородная функция.

В средах, где скорость волн - однородная функция лучи подобны друг другу и образуют группы подобных лучей. Также, оказывается, что лучи имеют параметр, - величину сохраняющуюся постоянной вдоль луча. В случае однородной скоростной функции порядок уравнения луча может быть понижен.

Уравнение поля времён в полярных координатах для среды, где скорость волн однородная функция, имеет вид:

(29)

Это нелинейное уравнение первого порядка в частных производных может быть сведено к двум обыкновенным дифференциальным уравнениям. Преобразуем переменные по формулам:

T = r ^{m - 1} t

R = ln (r)

отсюда

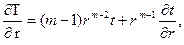
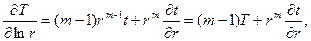
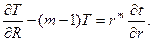
Умножим обе части уравнения поля времён на r ^{2 m}, получим:

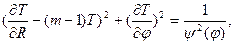
(30)

Обозначим ∂T/∂R = q, ∂T/∂ φ = р, (31)

Перепишем уравнение:

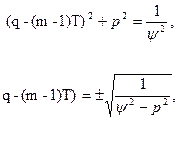
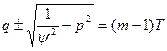
Будем искать решение в виде суммы двух функций:

T(R,j) = V (R) + U (j), (32)

получим:

или

Здесь φ, R - две независимые переменные. При любых значениях независимых переменных функции (левая и правая части уравнения) всегда равны друг другу. Значит обе части уравнения равны некоторой константе а, а - константа разделения.

(33)

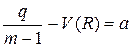
(34)

Решим уравнение (34).Оно интегрируется:

,

,

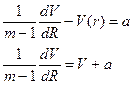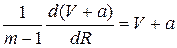
ln (V + a) = (m -1 ) R + C ₁,

V + a = C₁ e ^{(m- 1 )R} ,

V = C₁ e ^{( m- 1 )R} - a.

Рис.4.3.

Исследуем теперь уравнение (33)

Рассмотрим луч в полярной системе координат (рис. 26). Известно, что

êgrad t ê= 1 /v

Направление градиента поля времени совпадает с касательной к лучу. Введём угол i -образованный касательной к лучу с направлением нормали к прямой j = const. На рис.26 изображены составляющие градиента по осям полярной системы координат. Видно, что

или

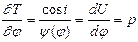(35)

Тогда уравнение (33) перепишется в виде

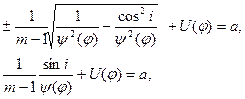
(36)

Выбор знака связан с направлением отсчета угла i, если так как показано на рис 23, то выбираем +.

Отсюда

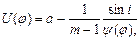
Заметим здесь, что функция sin i зависит только от j

Вернемся теперь к функции

Теперь вернемся к старым переменным r, t:

Разделим обе части уравнения на r ^{m- 1},получим:

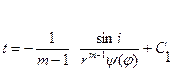
C ₁ найдём из условия - t (r ₀ ,j ₀ ) = 0, уравнение примет вид:

отсюда

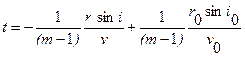₍₃₈₎

Если в формуле (38) положить t= const, получим уравнение фронта волны, если положить i ₀= cons t, получим уравнение луча (рис. 27). Для уравнения луча верно

(38а)

Выражение (38а)определяет величину, сохраняющую постоянное значение вдоль луча - параметр луча.

Дата добавления: 2014-01-07