Множество двухмерных возрастающих непрерывных однородных функций, есть замкнутый компакт

Легко видеть, что множество V двухмерных непрерывных однородных функций, которые увеличиваются с увеличением полярного угла

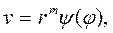(A1)

есть замкнутый компакт при условии

где A, B and C есть действительные числа.

Множество годографов T отвечающих двухмерным однородным функциям также являются замкнутым компактным множеством так как А есть непрерывный оператор. В работе Piip, 2001 показано, что временные поля, отвечающие скорости (A1) удовлетворяют уравнению

t = r^{1 - m} F(j, j₀, r/ r₀), (A2)

где r, φ and r ₀, φ ₀ являются координатами приемника и источника. Если j = j ₀ = 0 тогда уравнение (A2) описывает годографы на поверхности среды j= 0

t = r^{1 – m} T(r/ r₀). (A3)

Из уравнения (A3) следует, что t есть однородная функция степени (1- m) относительно r и r₀ и, следовательно, согласно теореме Эйлера

(A4)

Произведем замену переменных в (A4)

получим

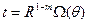, (A5)

здесь m есть действительное число, а Ω (Ө) есть произвольная функция.

Произведем следующую трансформацию функции (A5):

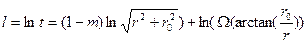, (A6)

Пусть 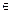l L,

Если r=r _0, тогда t =0, следовательно, мы должны ограничить область определения функции (A5)

0< E≤ R≤ F and 0 <G≤Ө≤ H<π /4, (A7)

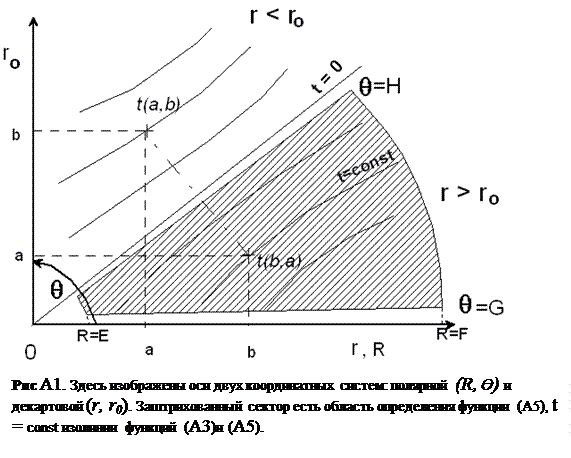
где E, F, G, H некоторые действительные числа (рис. 45).

Логарифмический оператор является непрерывным и однозначным при условии (A7),это означает, что мы получили взаимно-однозначное отображение множества T на множество L.

Для функции (A3) t(a,b)=t(b,a) (Рис. А1), согласно принципу взаимности, значит, область r>r ₀ есть зеркальное отображение области r<r ₀относительно оси r=r ₀. Тогда достаточно использовать для инверсии только годографы в области r> r ₀. Условие (A7) не ограничивает общность задачи, потому что при r=r _0, в случае любой функции v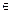V, мы имеем t= 0.

Область определения функции (A3) на плоскости изображения годографов в общепринятом виде показана на рис. А2.

Легко видеть, что L есть выпуклое множество. Известно (Ivanov, 1963), что в этом случае только единственная функция l ₀ =L наилучшим образом аппроксимирует ln y _δ и удовлетворяет уравнению

ρ (l, ln y_δ) = min.

Обратными преобразованиями к A6 мы получим единственное значение

t ₀=exp (l ₀).

Если ρ (t₀, y _δ ) <δ, любое решение x ₀ V уравнения

A x = t ₀

Будет лежать в ε-окрестности x:

ρ (x ₀, x) < ε,

согласно Иванову, (1963).

Таким образом, решение обратной кинематической задачи сейсмики на множестве двухмерных однородных функций, которые увеличиваются с увеличением полярного угла, устойчиво.

Литература

1. Аки К., Ричардс П. Количественная сейсмология. Теория и методы.Т.2. М. Мир.1983, 360с.
2. Елисеевнин В.А. Расчет лучей, распространяющихся в неоднородной среде. Акустический журнал, т.Х. вып.3, 1964.
3. Иванов В.К, 1963. О некорректно поставленных задачах. Математический сборник. т 61, N2, 211-223.
4. Кондратьев О.К., Гамбурцев А.Г. Сейсмические исследования в прибрежной Антарктиде. Изд-во АН СССР, М 1962
5. Облогина Т.И. Сейсморазведка неднородных сред. М. 1968 (учебное пособие).
6. .Пийп В.Б. Способ определения разреза в изолиниях скорости по годографам рефрагированных волн. Изв.АН СССР,Физика Земли. N 8, 1978, c 65-72.
7. .Пийп В.Б. Использование однородных функций для аппроксимации сейсмического скоростного разреза. Изв.АН СССР, Физика Земли. N 7, 1981, c 83-91.
8. Пийп В.Б. Новые методы интерпретации сейсмических временных полей в средах с переменными скоростями. Вестник Моск. Ун-та. сер.4 Геология,N3, 1984, c 83-92.
9. Пийп В.Б. Локальная реконструкция сейсмического разреза по данным преломленных волн на основе однородных функций. Физика Земли. № 10, 1991, с 24-32.
10. Пийп В.Б. Кинематика сейсмических волн в средах с однородной функцией скорости. М 1999 (учебное пособие).
11. Ċerveny V. Ray methods in seismic. Mathematical-Physical faculty in Karlovy University in Praha. 1978. 192p.

11. A new model of of the continental crust. In J. G. Heacock (Editor). The Earth crust (Geophysical Monograth 20). American Geological Union, Washington, D.C. pp.289 - 317, 1977.

Дата добавления: 2014-01-07