Управляемые идеальные источники

Управляемым (зависимым) источником называется такой источник электрической энергии, основной параметр (напряжение или ток) которого зависит от напряжений или токов в других участках цепи. Этот источник схематически можно представить четырехполюсником (см. рис. 1.13), у которого два полюса (1, 1¹) называют входными, а два других (2, 2¹) – выходными. Входной ток i₁ и входное напряжение u₁ являются управляющими величинами, а ток i₂ и напряжение u₂ – выходными управляемыми величинами. Различают четыре вида управляемых источников. Их эквивалентные схемы показаны на рис. 1.13.

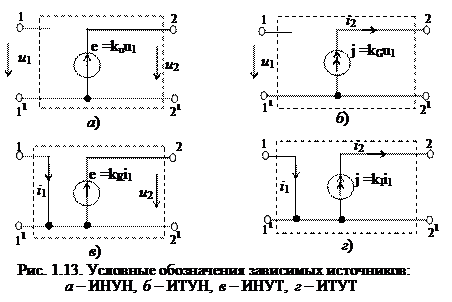1. ИНУН (рис. 1.13, а) – источник напряжения, управляемый напряжением. Входное сопротивление (входной ток i ₁ = 0), выходная проводимость велика (выходное сопротивление равно нулю), а выходное напряжение связано с входным равенством u₂ = e = k_uu₁, где k_u – коэффициент передачи по напряжению.

2. ИТУН (рис. 1.13, б) – источник тока, управляемый напряжением. Выходной ток i ₂ управляется входным напряжением u₁ по равенству

i₂=j= k_Gu₁,. где k _G – передаточная проводимость, имеющая размерность проводимости. Выходное сопротивление бесконечно велико.

3. ИНУТ (рис. 1.13, в) – источник напряжения, управляемый током. Входная проводимость бесконечна велика, выходное напряжение управляется входным током по равенству

u₂ = e = k_Ri₁,

где k _R – передаточное сопротивление, имеющее размерность сопротивления.

4. ИТУТ (рис. 1.13 г) – источник тока, управляемый током. Выходной ток i ₂ управляется входным током i₁ по равенству i₂=j= k_Ii₁,. где k _I – коэффициент передачи по току. Входная проводимость бесконечно велика. ИТУТ является идеальным усилителем тока.

Выражения выходных величин источников, выделенные в тексте, называют основными уравнениями управляемых источников. Коэффициенты k_U, k_G, k_R, k_I представляют собой вещественные положительные или отрицательные числа и полностью характеризуют источники.

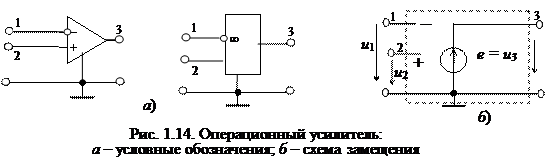Операционный усилитель (ОУ). Примером ИНУН является ОУ, выпускаемый промышленностью в виде отдельной микросхемы (рис. 1.14, а).

Операционный усилитель имеет два входа: 1 – инвертирующий и 2 – неинвертируещий. Они показываются на схеме соответствующим знаком («–» и «+» соответственно). При подаче напряжения u₁ на вход 1 – выходное напряженuе u₃ меняет свою полярность. Основным уравнением ОУ с двумя входами является

u₃ = e = k _U (u₂ – u₁). (1.13)

Идеальный ОУ отличается от ИНУН тем, что он имеет бесконечно большой коэффициент усиления (k _U = ∞), а выходное напряжение пропорционально разности входных напряжений. Также как и ИНУН ОУ имеет бесконечно большие входные сопротивления и выходную проводимость (выходное сопротивление равно нулю).

Так как коэффициент усиления k_U = ∞, то при конечном значении u₃ ОУ обладает важным свойством: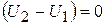, т. е. 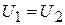или 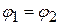, где φ₁ и φ₂ – потенциалы 1 и 2 полюсов ОУ.

Управляемые источники широко применяются при составлении моделей (эквивалентных схем замещения) активных элементов, например, электронных ламп, различных транзисторов (см. рис. 1.5, б), управляемых конденсаторов и др.

КЛАССИФИКАЦИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Электрические цепи могут быть классифицированы по ряду признаков:

– по энергетическим свойствам: активные (содержащие идеализированные активные элементы) и пассивные (не содержащие идеализированные активные элементы);

– по числу внешних полюсов: двухполюсники и др.(см. рис. 1.2, б);

– по типу пассивных элементов: резистивная цепь состоит только из резисторов R; реактивная цепь состоит только из L и C; RC – цепь; RL – цепь; RLC – цепь;

– по виду уравнений цепи:

а) если электрические процессы в цепи описываются линейными уравнениями с постоянными коэффициентами, то цепь называется линейной;

б) если электрические процессы в цепи описываются уравнениями с переменными во времени коэффициентами, то цепь называется параметрической;

в) если электрические процессы в цепи описываются нелинейными уравнениями, то цепь называется нелинейной.

Линейные цепи содержат только линейные элементы. Если в цепи находится хотя бы один нелинейный элемент, то вся цепь становится нелинейной. Если параметр какого-то элемента меняется во времени, то цепь является параметрической.

Фундаментальная классификация цепей строится в зависимости от вида дифференциального уравнения цепи.

Идеализированные цепи, процессы в которых описываются обыкновенными дифференциальными уравнениями, называются цепями с сосредоточенными параметрами. Цепи такого типа используют в качестве упрощенных моделей реальных цепей и их элементов на сравнительно низких частотах, когда длина волны электромагнитных колебаний существенно больше размеров исследуемого устройства. При этом условии в устройствах можно выделить конечное число участков, которые обладают каким-то одним из основных эффектов: R – преобразование электрической энергии, L или C – запасание энергии магнитного или электрического полей. Заменяя эти участки идеализированными элементами, получают модель реальной цепи, содержащей конечное число элементов, значения параметров которых конечны.

Когда длина волны колебаний соизмерима с размерами устройства или его элементов, пространственно локализовать области, в которых проявляются эффекты одного типа, не удается. Это связано с тем, что даже при бесконечно малой длине выделяемых участков, в пределах каждого из них одновременно имеют место несколько названных выше эффектов. Они (параметры) как бы «распределены» по всей цепи. Процессы в таких цепях описываются дифференциальными уравнениями в частных производных. Такие цепи называются цепями с распределенными параметрами.

В общем случае дифференциальное уравнение (ДУ) линейной цепи с сосредоточенными параметрами имеет вид:

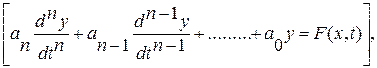(1.14)

где y(t) – отклик цепи (искомый ток или напряжение какой-либо ветви); a₀, a₁, … a_n – коэффициенты, определяемые параметрами пассивных элементов и коэффициентами управления зависимых источников; n – наибольшая степень производной. Правая часть уравнения (1.14) есть линейная комбинация функций, описывающих внешнее воздействие на цепьx = x(t), и их производных.

Наибольшее значение порядка (ДУ) цепи n характеризует порядок сложности (порядок цепи). Порядок цепи определяется числом реактивных элементов (емкостей и индуктивностей): n = 1 – цепь первого порядка и т.д.

ЗАКОНЫ КИРХГОФА

В теории цепей различают два типа задач: задачи анализа и синтеза цепей. К задачам анализа относятся все задачи, связанные с определением токов, напряжений (откликов) в элементах цепи, если схема и параметры элементов заданы. В задачах синтеза, напротив – известны токи и напряжения в отдельных элементах и требуется определить вид цепи и ее параметры.

В основе методов анализа цепей лежат законы Кирхгофа.

Первый закон Кирхгофа – закон токов в узлах. Он отражает тот факт, что в узлах не могут накапливаться заряды. Он гласит:

алгебраическая сумма токов ветвей, сходящихся в любом узле цепи, равна нулю

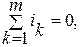(1.15)

где m – число ветвей, сходящихся в узле.

Второй закон Кирхгофа – закон напряжений в контуре. Он гласит:

алгебраическая сумма напряжений ветвей в любом контуре равна нулю

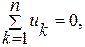(1.16

где n – число ветвей, входящих в контур.

Практическое применение законов Кирхгофа рассматривается на практических занятиях по курсу ОТЦ.

МЕТОДЫ АНАЛИЗА СЛОЖНЫХ ЦЕПЕЙ

В дальнейшем будем называть сложными такие цепи, которые содержат более одного контура. Полный анализ сложной цепи заключается в нахождении токов всех ветвей или, что равноценно, в определении потенциалов всех ее узлов, т.е. напряжений между узлами.

На практических занятиях рассматриваются различные методы анализа линейных цепей.

Дата добавления: 2014-01-07