
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоремы булевой алгебры
|
|
|
|
| №:п/п | Дизъюнкция | Конъюнкция | Примечание |
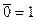
| 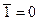
| Аксиомы | |
| х + 0 = х | х ·1 = х | ||
| х + 1 = 1 | х ·0 = 0 | ||
| х + х = х | х·х = х | ||
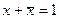
| 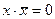
| ||
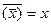
| Закон двойного отрицания | ||
| x + у = у + х | x у = у х | Закон коммутативности | |
x + х у = х
х + 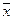 у = х + у у = х + у
| х (х + у) = х
х (у +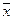 ) = х у ) = х у
| Закон поглощения | |
x y + x 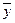 = x = x
| (x + y)(x +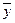 ) = x ) = x
| Закон склеивания | |
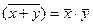
| 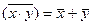
| Закон де Моргана | |
| (х + у) + z = = x + (y + z) = x + y + z | (x y) z = x (y z) = x y z | Закон ассоциативности | |
| x + y z = (x + y) (x + z) | x (y + z) = x y + x z | Закон дистрибутивности |
Наиболее употребительны при упрощении структурных формул законы поглощения и склеивания.
Убедиться в справедливости приведенных законов булевой алгебры нетрудно путем подстановки в правую часть и в левую часть формул всех возможных комбинаций переменных.
3.3. Совершенные нормальные формы
Ранее рассмотренные таблицы истинности и структурные формулы являются различными формами описания одних и тех же булевых функций. Поэтому иногда возникает необходимость перехода от одной формы описания к другой.
Переход от структурной формулы к соответствующей ей таблице истинности не вызывает затруднений. Для получения таблицы истинности достаточно подставить в структурную формулу вместо переменных все возможные наборы их значений и определить для каждого из них значение функции.
Минтермы и макстермы. Прежде чем сформулировать правила получения аналитической записи булевой функции, заданной таблично, введем некоторые новые понятия.
Логические произведения аргументов булевой функции, взятых с инверсией или без нее, называют элементарными конъюнкциями. Так, например, функция f 1(x 2 ,x 1 ,x 0) = x 2 x 1 является элементарной конъюнкцией, а f 2(x 2 ,x 1 ,x 0) = 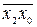 – нет. Количество сомножителей в элементарной конъюнкции называется ее рангом.
– нет. Количество сомножителей в элементарной конъюнкции называется ее рангом.
Две элементарные конъюнкции одинакового ранга называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания одного из сомножителей.
Элементарное произведение, являющееся функцией всех переменных булевой функции, называют минтермом. Для функции n переменных существует 2 n минтермов.
Логическая сумма аргументов булевой функции, взятых со знаком инверсии или без него, называется элементарной дизъюнкцией. Элементарная дизъюнкция, являющаяся функцией всех переменных булевой функции, называется макстермом. Для булевой функции n переменных можно составить 2 n макстермов.
Количество слагаемых в элементарной дизъюнкции называется ее рангом. Две элементарные дизъюнкции одинакового ранга называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком инверсии одного из слагаемых.
Совершенные дизъюнктивная и конъюнктивная нормальные формы. Структурная формула булевой функции может быть записана в совершенной дизъюнктивной нормальной форме (СДНФ) и в совершенной конъюнктивной нормальной форме (СКНФ).
Структурная формула булевой функции в СДНФ представляет собой логическую сумму ее минтермов, записанных для тех наборов значений аргументов функции, на которых она принимает единичное значение. В дальнейшем такие наборы будем называть единичными.
Для составления структурной формулы булевой функции в СДНФ по ее таблице истинности достаточно записать дизъюнкцию минтермов для всех единичных наборов функции. При этом символ любой переменной этой функции в минтерме берется со знаком отрицания (инверсии), если конкретное значение этой переменной в рассматриваемом наборе равно 0.
Поясним сказанное на примере. Пусть булева функция y ' = = f (x 3, x 2, x 1, x 0) задана таблицей истинности (табл. 3.4). Структурная формула этой функции в СДНФ
y´= 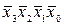 +
+ 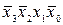 +
+ 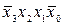 +
+ 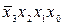 +
+
+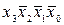 +
+ 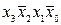 +
+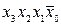 +
+ 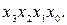 (3.1)
(3.1)
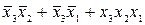 ,
,
у'' = 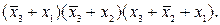
Табличный метод минимизации булевых функций очень удобен при числе аргументов, не превышающих пять. При шести и большем числе переменных этот метод минимизации становится громоздким. В этом случае применяются табличные способы минимизации, позволяющие использовать точные компьютерные методы. В данной книге эти методы минимизации не рассматриваются.
 |
Лекция 4
 ЛОГИЧЕСКИЕ ИНТЕГРАЛЬНЫЕ СХЕМЫ
ЛОГИЧЕСКИЕ ИНТЕГРАЛЬНЫЕ СХЕМЫ
Для уменьшения объема, веса, потребляемой энергии и стоимости при одновременном повышении надежности и быстродействия в конце 50-х годов прошлого века была выдвинута идея совместного изготовления радиоэлектронных элементов и их взаимных соединений. Развитие этой идеи явилось началом нового направления в радиоэлектронике, получившего название микроэлектроники. Разработанный в результате метод изготовления в общем технологическом цикле всей совокупности элементов схемы и их соединений получил название метода интеграции элементов, а создаваемые миниатюрные схемы стали называть интегральными микросхемами или просто интегральными схемами (ИС).
Классификация ИС по выполняемым функциям основывается на их делении на два основных класса – аналоговые и цифровые.
Аналоговые ИС предназначены для преобразования и обработки аналоговых сигналов.
К цифровым относятся ИС, предназначенные для преобразования и обработки цифровых сигналов.
Особым видом ИС являются ИС цифро-аналоговых преобразователей и аналого-цифровых преобразователей, предназначенных для преобразования соответственно цифровых сигналов в аналоговые сигналы и аналоговых сигналов в цифровые.
Изготовление цифровых устройств в интегральном исполнении способствует повышению их эффективности как за счет непосредственного увеличения функциональной емкости единицы объема (например, число бит памяти в единице объема), так и за счет увеличения быстродействия устройств. С уменьшением размеров элементов уменьшаются их паразитные емкости, а уменьшение расстояния между элементами приводит к уменьшению времени передачи сигналов.
В настоящее время насчитывается огромное число разновидностей цифровых ИС. Их обновление происходит исключительно высокими темпами в направлении увеличения быстродействия, снижения потребляемой мощности, расширения логических возможностей, снижения стоимости, повышения надежности за счет:
– совершенствования схемного решения ЛЭ (уменьшения размеров и числа компонентов в ЛЭ, изменения режимов его работы);
– совершенствования технологии, приводящей к снижению геометрических размеров элементов и, следовательно, к повышению быстродействия;
– применения новых материалов, например арсенида галлия.
Комплект ИС, имеющих единое конструктивно-технологическое исполнение, принято называть серией.
4.1. Параметры логических ИС
 Ниже рассмотрены основные параметры цифровых ИС.
Ниже рассмотрены основные параметры цифровых ИС.
 Время задержки распространения сигнала внутри ИС при ее переключении из состояния логической единицы в состояние логического нуля t
Время задержки распространения сигнала внутри ИС при ее переключении из состояния логической единицы в состояние логического нуля t 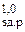 представляет собой интервал времени между выходным и входным сигналами при переходе выходного сигнала ИС от напряжения высокого уровня к напряжению низкого уровня. Интервал времени измеряется на уровне 0,5 напряжений входного и выходного сигналов (рис. 4.1).
представляет собой интервал времени между выходным и входным сигналами при переходе выходного сигнала ИС от напряжения высокого уровня к напряжению низкого уровня. Интервал времени измеряется на уровне 0,5 напряжений входного и выходного сигналов (рис. 4.1).
Время задержки распространения сигнала внутри ИС при ее переключении из состояния логического нуля в состояние логической единицы t 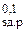 представляет собой интервал времени между выходным и входным сигналами при переходе выходного сигнала ИС от напряжения низкого уровня к напряжению высокого уровня. Интервал времени измеряется на уровне 0,5 напряжений входного и выходного сигналов (рис. 4.1).
представляет собой интервал времени между выходным и входным сигналами при переходе выходного сигнала ИС от напряжения низкого уровня к напряжению высокого уровня. Интервал времени измеряется на уровне 0,5 напряжений входного и выходного сигналов (рис. 4.1).
Время перехода ИС из состояния логической единицы в состояние логического нуля (длительность среза импульса) t 1,0 определяется как интервал времени, в течение которого напряжение на выходе ИС переходит от напряжения высокого уровня к напряжению низкого уровня. Интервал времени измеряется на уровнях 0,9 и 0,1 напряжения выходного сигнала (рис. 4.1).
Время перехода ИС из состояния логического нуля в состояние логической единицы (длительность фронта импульса) t 0,1 определяется как интервал времени, в течение которого напряжение на выходе ИС переходит от напряжения низкого уровня к напряжению высокого уровня. Интервал времени измеряется на уровнях 0,1 и 0,9 напряжения выходного сигнала (рис. 4.1).
Основной оценкой быстродействия ИС является с реднее время задержки распространения сигнала t 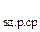 = (t
= (t 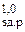 + t
+ t 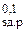 )/2.
)/2.
Помехоустойчивость характеризуется наибольшим значением напряжения помехи U пом, воздействие которой на вход ИС не вызывает ее ложного срабатывания.
Для более полной оценки помехоустойчивости ИС наряду со статической помехоустойчивостью необходимо учитывать ее помехоустойчивость в динамическом режиме. Динамическая помехоустойчивость ИС определяется длительностью, амплитудой и формой помехи и зависит от ее статической помехоустойчивости.
Нагрузочная способность (коэффициент разветвления по выходу) определяется числом аналогичных схем, которые могут быть подключены к выходу данной схемы без нарушения ее работоспособности.
Коэффициент объединения по входу определяется числом входов ИС, по которым реализуется логическая функция.
Потребляемая мощность Р потр – это мощность, потребляемая ИС от источника питания. Так как потребляемая мощность оказывается максимальной в момент переключения ИС, ее измерение производится в динамическом режиме при подаче на вход управляющих импульсов определенной частоты.
Энергия переключения ИС – величина, равная произведению среднего времени задержки распространения сигнала и потребляемой мощности, т. е. Э = t 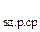 ∙ Р потр. Этот параметр используется для сравнения ИС различных серий. Для идеального ЛЭ должны быть малыми как потребляемая мощность, так и время задержки распространения сигнала. Поэтому принято считать, что чем ниже величина энергии переключения, тем лучше серия ИС.
∙ Р потр. Этот параметр используется для сравнения ИС различных серий. Для идеального ЛЭ должны быть малыми как потребляемая мощность, так и время задержки распространения сигнала. Поэтому принято считать, что чем ниже величина энергии переключения, тем лучше серия ИС.
4.2. Интегральные схемы транзисторно-транзисторной
логики
Интегральные схемы транзисторно-транзисторной логики в настоящее время широко используются в качестве элементной базы цифровых устройств. Существуют две разновидности транзисторно-транзисторной логики:
– транзисторно-транзисторная логика без диодов Шоттки (ТТЛ);
– транзисторно-транзисторная логика с диодами Шоттки (ТТЛШ).
Рассмотрим принцип работы ИС первой разновидности транзисторно-транзисторной логики на примере ЛЭ И-НЕ ИС серии К155. Схема этого ЛЭ приведена на рис. 4.2.
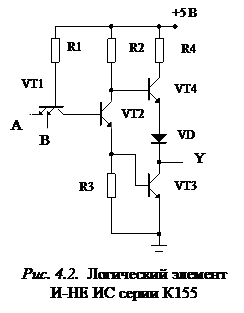 Схема содержит три основных каскада: входной на транзисторе VТ 1, фазоразделительный на транзисторе VТ 2 и выходной на транзисторах VТ 3 и VТ 4.
Схема содержит три основных каскада: входной на транзисторе VТ 1, фазоразделительный на транзисторе VТ 2 и выходной на транзисторах VТ 3 и VТ 4.
Входной каскад рассматриваемого ЛЭ комбинирует входные сигналы и определяет реализуемую булеву функцию. С целью повышения быстродействия он выполнен на основе многоэмиттерного транзистора, имеющего низкое входное сопротивление. Основное структурное отличие многоэмиттерного транзистора от обычного биполярного транзистора заключается в наличии нескольких (в рассматриваемой схеме двух) независимых эмиттеров и общих для них базы и коллектора. При этом транзистор выполнен таким образом, что прямое взаимодействие между эмиттерами через разъединяющий их участок базы практически исключается.
Фазоразделительный каскад, реализованный на транзисторе VT 2, обеспечивает в любой момент времени открытое состояние транзистора VT 3 и закрытое состояние транзистора VT 4 либо открытое состояние транзистора VT 4 и закрытое состояние транзистора VT 3. Это позволяет выбрать малое сопротивление резистора R 4. Поэтому ЛЭ имеет низкое выходное сопротивление при формировании на выходе как логического нуля, так и логической единицы. Это способствует увеличению быстродействия ЛЭ благодаря уменьшению времени перезаряда паразитных емкостей, подключенных к выходу ЛЭ.
Если на оба входа А и В одновременно поданы напряжения высокого уровня (лог. 1), обе транзисторные структуры транзистора VТ 1 находятся в инверсном режиме, так как его эмиттерные переходы смещены в обратном направлении, а коллекторный переход – в прямом. Коллекторный ток транзистора VТ 1 открывает транзистор VТ 2, в результате чего транзистор VТ 3 переводится в проводящее состояние, а транзистор VТ 4 – в закрытое состояние (режим отсечки) и на выходе формируется напряжение низкого уровня (лог. 0). При появлении, по крайней мере, на одном входе напряжения низкого уровня соответствующая транзисторная структура транзистора VТ 1 переходит в режим насыщения. При этом на его коллекторе формируется низкий потенциал, транзисторы VТ 2 и VТ З переводятся в режим отсечки, а транзистор VТ 4 – в проводящее состояние и на выходе базового логического элемента формируется напряжение высокого уровня. Таким образом,  .
.
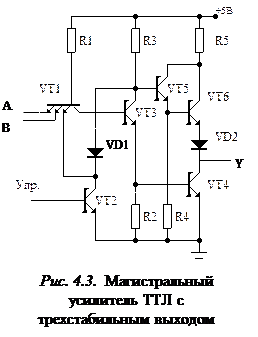 Малое выходное сопротивление рассмотренных ЛЭ исключает возможность их объединения по выходу. Указанного недостатка лишена схема магистрального усилителя ТТЛ с трехстабильным выходом (рис. 4.3), отличающаяся от предыдущей схемы наличием состояния с высоким выходным сопротивлением.
Малое выходное сопротивление рассмотренных ЛЭ исключает возможность их объединения по выходу. Указанного недостатка лишена схема магистрального усилителя ТТЛ с трехстабильным выходом (рис. 4.3), отличающаяся от предыдущей схемы наличием состояния с высоким выходным сопротивлением.
Перевод схемы в это состояние обеспечивается подачей на управляющий вход Упр напряжения высокого уровня, переводящего транзистор VТ 2 в проводящее состояние и удерживающего транзистор VТ 1 в режиме насыщения, а транзисторы VТ З и VT 4 – в режиме отсечки. В то же время открытый транзистор VТ 2 шунтирует коллекторную цепь транзистора VТ 3, благодаря чему транзисторы VТ 5 и VТ 6 также будут закрыты. В этом случае выход схемы находится в третьем состоянии – состоянии высокого выходного сопротивления. При наличии напряжения низкого уровня на управляющем входе состояние выхода этой схемы определяется состоянием ее информационных входов А и В.
Основными недостатками ИС серии К155 являются большая потребляемая мощность и большая задержка распространения сигналов (табл. 4.1). Предпринимались попытки уменьшить потребляемую мощность (ИС серии К134) путем увеличения сопротивлений резисторов R 1, R 2 и R 4 (рис. 4.2) и увеличить быстродействие (ИС серии К131) путем уменьшения сопротивлений этих же резисторов. Однако эти попытки не увенчались успехом, так как уменьшение потребляемой мощности сопровождалось снижением быстродействия, а увеличение быстродействия приводило к увеличению потребляемой мощности (табл. 4.1). Поэтому в 70-х годах прошлого века ИС ТТЛ стали активно заменяться ИС ТТЛ с диодами Шоттки (ТТЛШ). В настоящее время ИС серий К155, К134 и К131 сняты с производства.
Логические элементы ИС серий К155, К134, К131 относятся к так называемым насыщенным логическим элементам, поскольку их транзисторы в проводящем состоянии находятся в режиме насыщения. Ограничение быстродействия таких ЛЭ в первую очередь обусловлено процессами накопления избыточного заряда в базах насыщенных транзисторов и рассасывания этого заряда при их закрывании.
| Таблица 4.1 Основные параметры ИМС ТТЛ | |||
| Серия ИС | Р потр, мВт | t зд.р.ср, нс. | Э, пкДж |
| К155 ─ ТТЛ К134 ─ маломощная ТТЛ К131 ─ быстродействующая ТТЛ К531 ─ ТТЛШ К555 ─ маломощная ТТЛШ КР1533 ─ маломощная быстродействующая ТТЛШ КР1531 ─ сверхбыстродействующая ТТЛШ | 1,0 | 10,0 33,0 6,0 3,0 9,5 4,0 2,0 |
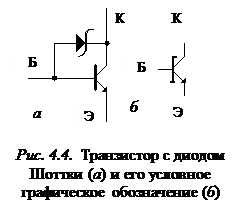 Для преодоления этого недостатка были разработаны серии микросхем с диодами Шоттки, включенными параллельно коллекторному переходу (рис. 4.4). При открывании такого транзистора на коллекторе установится потенциал, переводящий диод Шоттки в проводящее состояние. Падение напряжения на диоде Шоттки в этом состоянии не превышает (0,3 ¸ 0,4) В, т. е. меньше, чем падение напряжения на открытом переходе база – коллектор и, следовательно, диод откроется раньше, чем переход база – коллектор. Переход оказывается закрытым, и режим насыщения исключается. Кроме того, сами диоды Шоттки являются очень быстродействующими диодами, что и обеспечивает эффективность такой нелинейной обратной связи. Такие транзисторы получили название транзисторов Шоттки.
Для преодоления этого недостатка были разработаны серии микросхем с диодами Шоттки, включенными параллельно коллекторному переходу (рис. 4.4). При открывании такого транзистора на коллекторе установится потенциал, переводящий диод Шоттки в проводящее состояние. Падение напряжения на диоде Шоттки в этом состоянии не превышает (0,3 ¸ 0,4) В, т. е. меньше, чем падение напряжения на открытом переходе база – коллектор и, следовательно, диод откроется раньше, чем переход база – коллектор. Переход оказывается закрытым, и режим насыщения исключается. Кроме того, сами диоды Шоттки являются очень быстродействующими диодами, что и обеспечивает эффективность такой нелинейной обратной связи. Такие транзисторы получили название транзисторов Шоттки.
На основе транзисторов Шоттки выпускаются ИС транзисторно-транзис-торной логики с диодами Шотки (ТТЛШ).
На рис. 4.5 приведена схема логического элемента И-НЕ серии К531. В этом ЛЭ с целью уменьшения потребляемой мощности в случае формирования на выходе ЛЭ высокого напряжения (лог. 1) резистор R 5 подключен не к общей шине, а к выходу элемента. В качестве эмиттерной нагрузки транзистора VТ 2 используется генератор тока, построенный на транзисторе VТ 3. Применение транзисторов Шоттки позволило за счет работы транзисторов в ненасыщенном режиме снизить задержку распространения сигнала до 3 нс.
Наиболее перспективными в настоящее время из всех ИС ТТЛ являются серии:
 – К555 – маломощная ТТЛШ;
– К555 – маломощная ТТЛШ;
– КР1533 – маломощная быстродействующая ТТЛШ;
– КР1531 – сверхбыстродействующая ТТЛШ.
Увеличение сопротивлений резисторов R 1, R 3, R 6 (рис. 4.5) в так называемой экономичной (маломощной) серии К555 ТЛШ привело к уменьшению по сравнению с ИС серии 531 потребляемой мощности почти на порядок и к некоторому снижению быстродействия (табл. 4.1).
ИС серии КР1533 по сравнению с известными сериями ИС ТТЛ обладают минимальным значением энергии переключения. Схема ЛЭ И-НЕ серии КР1533 приведена на рис. 4.6. Он содержит три основных каскада:
– входной (транзисторы VT 1, VT 2 и VT 3, диоды VD 1 и VD 3, резисторы R 1 и R 2);
– фазоразделительный (транзисторы VT 4 и VT 5, диоды VD 2 и VD 4, резисторы R 3, R 5 и R 6);
– выходной (транзисторы VT 6 ÷ VT 8, диоды VD 5 ÷ VD 7, резисторы R 4, R 7).
На входе элемента использованы p – n – p -транзисторы VT 1 и VT 2, что позволило повысить нагрузочную способность в результате уменьшения входного тока и увеличить быстродействие путем использования p – n – p -транзисторов, работающих в активном режиме.
При низком напряжении, по крайней мере, на одном входе ЛЭ на базе транзистора VT 3 поддерживается низкое напряжение, транзисторы VT 3 ÷ VT 5 закрыты, а транзисторы VT 6 и VT 7 открыты. На выходе ЛЭ устанавливается напряжение высокого уровня.
При высоком напряжении на обоих входах ЛЭ эмиттерные переходы транзисторов VT 1 и VT 2 закрыты, транзистор VT 3 и, следовательно, транзисторы VT 4 и VT 8 открыты. Транзисторы VT 6 и VT 7 закрыты, и на выходе ЛЭ устанавливается напряжение низкого уровня. Таким образом, рассмотренный ЛЭ является двухвходовым ЛЭ И-НЕ.
ИС серии КР1531 по сравнению с известными сериями ИС ТТЛ обладают минимальным значением среднего времени задержки распространения сигнала при сравнительно небольшом значении энергии переключения (табл. 4.1). Такие результаты получены в основном благодаря применению изопланарной технологии, позволившей уменьшить размеры элементов и снизить барьерную емкость p – n -переходов.

4.3. Интегральные схемы эмиттерно-связанной
логики
Интегральные схемы эмиттерно-связанной логики (ЭСЛ) строятся на переключателях тока, представляющих собой ключевые элементы на транзисторах с объединенными эмиттерами. Большое быстродействие в таких схемах достигается за счет работы транзисторов в ненасыщенном режиме, выбора сравнительно небольшого (порядка 1 В) перепада выходных напряжений, а также применения выходных эмиттерных повторителей, ускоряющих процессы заряда и разряда паразитных емкостей цепи нагрузки.
Основными недостатками ИС ЭСЛ является малая величина перепада выходных напряжений и сравнительно низкая помехоустойчивость.
Так как питание ИС ЭСЛ производится от источника постоянного тока с отрицательным напряжением –5,2 В, то выходное напряжение ЛЭ является отрицательным. В качестве напряжений логического нуля и логической единицы выбирают соответственно низкий и высокий от
рицательные уровни выходного напряжения.
Схема ЛЭ 2И/2И-НЕ ЭСЛ (рис. 4.7) состоит из переключателя тока, собранного на транзисторах VТ 1 ÷ VТ 3, источника опорного напряжения, построенного на транзисторе VТ 4 и термокомпенсирующих диодах VД 1 и VД 2, и выходных эмиттерных повторителей, выполненных на транзисторах VТ 5 и VТ 6.
Входные сигналы сравниваются с опорным напряжением U ОП = = –1,3 В, относительно которого и происходит переключение транзисторов переключателя тока. Если на входах А и В присутствует напряжение логической единицы, в качестве которого выбрано напряжение –1,7 В, транзисторы VТ 1 и VТ 2 закрыты и весь ток генератора постоянного тока, образованного эмиттерным сопротивлением R 4 и источником питания –5,2 В, протекает через открытый транзистор VТ 3. При этом на эмиттере транзистора VТ 6 формируется напряжение логического нуля (порядка –1 В), а на эмиттере транзистора VТ 5 – напряжение логической единицы.
Появляющееся, по крайней мере, на одном из входов ЛЭ напряжение логического нуля открывает соответствующий транзистор (VТ 1 или VТ 2) и закрывает транзистор VТ 3. В этом случае напряжение логического нуля формируется на эмиттере транзистора VТ 5, а напряжение логической единицы – на эмиттере транзистора VТ 6. Таким образом, рассмотренная схема по одному выходу реализует функцию И, а по другому – И-НE.
Как уже отмечалось, ИС ЭСЛ являются наиболее быстродействующими логическими схемами. В базовом логическом элементе ИС ЭСЛ среднее время задержки распространения сигнала t  достигает величины, приблизительно равной (0,7–1) нс. Такое быстродействие достигнуто ценой увеличения потребляемой мощности до (30–50) мВт.
достигает величины, приблизительно равной (0,7–1) нс. Такое быстродействие достигнуто ценой увеличения потребляемой мощности до (30–50) мВт.
Появление быстродействующих ИС ТТЛ и ИС на КМОП-тран-зисторах сделало бесперспективным дальнейшее развитие цифровых ИС ЭСЛ.
4.4. Логические схемы на полевых транзисторах
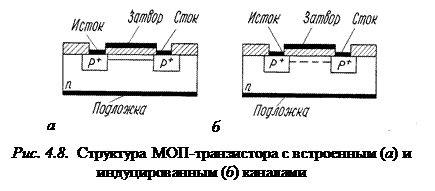 |
ИС на полевых транзисторах получили широкое распространение. Благодаря хорошей технологичности, высокой степени интеграции, малой стоимости и малой мощности потребления они стали незаменимыми при производстве больших интегральных схем запоминающих устройств и микроконтроллеров. В логических схемах наибольшее применение находят полевые транзисторы со структурой металл – оксид – полупроводник (МОП-транзистор). Существуют МОП-транзисторы с встроенным каналом и МОП-транзисторы с индуцированным каналом. Транзисторы первого типа (рис. 4.8, а) являются нормально открытыми транзисторами, то есть при нулевом напряжении на затворе относительно истока канал имеет сравнительно малое сопротивление. МОП-транзисторы с индуцированным каналом (рис. 4.8, б) являются нормально закрытыми, т. е. при нулевом напряжении на затворе канал отсутствует и транзистор находится в непроводящем состоянии. Только при подаче на затвор отпирающего потенциала между стоком и истоком формируется (индуцируется) канал, и транзистор переходит в проводящее состояние. Минимальное напряжение на затворе, достаточное для образования канала, называется пороговым напряжением. Большинство выпускаемых в настоящее время логических ИС на МОП-структурах основано на МОП-тран-зисторах с индуцированным каналом.
4.4.1. Логические схемы на МОП-транзисторах с каналами
одинаковой проводимости
Для реализации различных логических функций используют последовательно-параллельное соединение р -канальных или n- канальных транзисторов, действующих как переключатели. Если напряжение на затворе МОП-транзистора с индуцированным каналом (рис. 4.9) превышает пороговое напряжение, переключатель замкнут. При нулевом напряжении на его входе переключатель разомкнут.
 На рис. 4.10 приведена схема логического элемента 2И-НЕ в отрицательной логике. Она содержит два переключателя на транзисторах VТ1 и VТ2 и один нагрузочный транзистор VТ3. Этот транзистор открыт постоянно, однако ток через него протекает лишь при наличии на входах А и В напряжения низкого уровня. При этом на выходе Y формируется напряжение высокого уровня.
На рис. 4.10 приведена схема логического элемента 2И-НЕ в отрицательной логике. Она содержит два переключателя на транзисторах VТ1 и VТ2 и один нагрузочный транзистор VТ3. Этот транзистор открыт постоянно, однако ток через него протекает лишь при наличии на входах А и В напряжения низкого уровня. При этом на выходе Y формируется напряжение высокого уровня.
На смену разработанной вначале технологии р -канальных МОП-транзисторов, не обеспечивающих должного быстродействия и удовлетворительной степени интеграции ИС, пришла технология более быстродействующих и компактных, совместимых по электрическим уровням со схемами ТТЛ n -канальных структур.
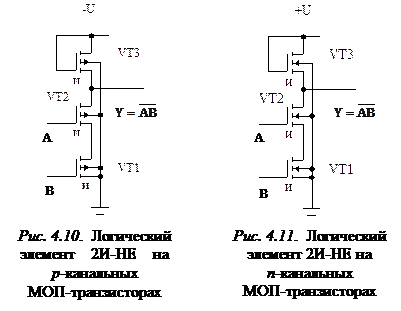 |
Принципиальная схема логического элемента 2И-НЕ на n -каналь-ных МОП-транзисторах с индуцированным каналом приведена на рис. 4.11. Если напряжение на входе хотя бы одного из транзисторов VТ 1 или VТ 2 меньше порогового напряжения используемого МОП-тран-зистора, то этот транзистор остается закрытым и на выходе Y формируется напряжение высокого уровня, соответствующее в положительной логике логической единице. Только при одновременном появлении на входах А и В напряжений, превышающих пороговое напряжение, открываются оба транзистора и через нагрузочный транзистор VТ 3 протекает ток, обеспечивающий формирование на выходе напряжения низкого уровня, соответствующего логическому нулю.
Схемы ИЛИ-НЕ на МОП-транзисторах с каналами одного типа образуются параллельным соединением переключаемых транзисторов и подсоединением их объединенных стоков к истоку нагрузочного транзистора.
4.4.2. Логические схемы на КМОП-транзисторах
В логических схемах на КМОП-транзисторах для реализации основных логических функций используются пары комплементарных МОП-транзисторов (КМОП-транзисторов): один p -канальный, а второй – n -канальный. Схема инвертора на двух последовательно включенных КМОП-транзисторах приведена на рис. 4.12. При поступлении на его вход напряжения высокого уровня, превышающего пороговое напряжение транзистора VТ 1 и соответствующего логической единице в положительной логике, транзистор VТ 1 открывается, а транзистор VT 2 закрывается и на выходе формируется напряжение низкого уровня, соответствующее логическому нулю. При поступлении на вход инвертора напряжения низкого уровня транзистор VТ 1 закрывается, а транзистор VТ 2 открывается, благодаря чему на выходе инвертора формируется напряжение высокого уровня.
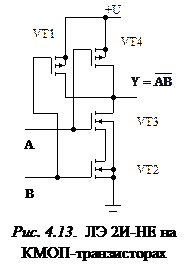
 Для реализации функции И-НЕ используют параллельное включение МОП-транзисторов р -типа и последовательное включение
Для реализации функции И-НЕ используют параллельное включение МОП-транзисторов р -типа и последовательное включение
МОП-транзисторов n -типа. При этом каждый из транзисторов р -типа связан по затвору с транзистором n -типа (рис. 4.13). При подаче на оба входа напряжения высокого уровня транзисторы VТ 1 и VТ 4 закрываются, а транзисторы VТ 2 и VТ 3 открываются, и на выходе формируется напряжение низкого уровня. При поступлении на один из входов (или одновременно на оба) напряжения низкого уровня один из транзисторов VТ 2 или VТ 3 (или оба одновременно) закрывается, а один из транзисторов VТ 1 или VТ 4 (или оба одновременно) открывается, и на выходе формируется напряжение высокого уровня.
Основное достоинство ИС на КМОП-транзисторах – это предельно низкая потребляемая мощность. Ток потребления в статическом режиме КМОП ЛЭ определяется током утечки закрытых n - и p -канальных МОП-транзисторов. Величина этого тока приблизительно на три порядка меньше, чем у ИС маломощной быстродействующей ТТЛШ КР1533.
 Потребляемая мощность заметно возрастает при работе ИС на КМОП-транзисторах в динамическом режиме. Возрастание потребляемой мощности с увеличением частоты переключений ИС обусловлено в первую очередь перезарядом при переключении внутренних емкостей ИС. Кроме того, при переключении схемы в течение некоторого времени оба транзистора с n -каналом и р -каналом могут находиться в открытом состоянии, что приводит к возникновению кратковременных бросков тока.
Потребляемая мощность заметно возрастает при работе ИС на КМОП-транзисторах в динамическом режиме. Возрастание потребляемой мощности с увеличением частоты переключений ИС обусловлено в первую очередь перезарядом при переключении внутренних емкостей ИС. Кроме того, при переключении схемы в течение некоторого времени оба транзистора с n -каналом и р -каналом могут находиться в открытом состоянии, что приводит к возникновению кратковременных бросков тока.
Биполярные ИС и ИС на КМОП-тран-зисторах на высоких частотах имеют примерно одинаковые показатели тепловыделения, но КМОП ИС более технологичны, что и определило их преобладание в больших интегральных схемах.
Еще одно достоинство – высокое быстродействие. Время задержки распространения сигнала ИС на КМОП-транзисторах стало сопоставимо со временем задержки распространения сигнала лучшими ИС ЭСЛ. В настоящий момент можно говорить о возможности применения ИС на КМОП-транзисторах в цифровых системах самого высокого быстродействия.
В отличие от биполярных ИС ИС на КМОП-транзисторах способны работать в широком диапазоне питающих напряжений. Диапазон напряжения питания, в котором гарантируются характеристики ИС, для многих серий ИС на КМОП-транзисторах – от 3 В до 5,5 В.
Высокое быстродействие ИС на КМОП-транзисторах в сочетании с достаточно широким диапазоном напряжений питания, низкой потребляемой мощностью, большой нагрузочной способностью и хорошей помехоустойчивостью, работой в широком диапазоне температур объясняет наибольшую популярность ИС этого типа.
4.5. Структура элементной базы цифровых устройств
Все выпускаемые в настоящее время интегральные схемы можно разделить на две группы: стандартные ИС и специализированные ИС (рис. 4.14). Стандартные ИС, как правило, разрабатываются по инициативе производителя и выпускаются большими тиражами. Это микросхемы памяти и элементы малой и средней степени интеграции: вентили, регистры, шифраторы, дешифраторы, мультиплексоры и др.
 |
Специализированные ИС принято делить на три класса: полностью заказные, полузаказные и программируемые пользователем.
Разработка полностью заказных ИС охватывает полный цикл проектирования, что обеспечивает наилучшие характеристики устройства, но увеличивает время разработки и подготовки производства до нескольких лет. Значительное удорожание изделия компенсируется большими объемами его производства.
Построение ИС на основе базовых структур полузаказных ИС, представляющих собой матрицы нескоммутированных между собой элементов, электрические связи между которыми формируются в соответствии с назначением ИС на последних этапах их изготовления, позволяет значительно снизить стоимость цифровых устройств. Время разработки цифровых устройств на основе базовых структур полузаказных ИС может составлять от нескольких недель до нескольких месяцев. Типичными представителями полузаказных ИС являются стандартные ячейки (Standart Cells – SC) и вентильные матрицы (Gate Arrays – GA).
Наибольшей оперативностью и гибкостью использования характеризуются ИС, программируемые пользователем. Стоимость и время разработки при этом минимальны.
Программируемые пользователем ИС можно разделить на микропрограммные ИС и программируемую логику (ПЛИС) в соответствии с двумя основными подходами к проектированию цифровых устройств: микропрограммным и аппаратным. Первый подход предполагает построение цифровых устройств на базе некоторого универсального элемента (микропроцессора, микроконтроллера и др.), который специализируется загружаемой в ОЗУ или зашиваемой в ППЗУ программой.
Характерной особенностью ПЛИС является возможность их настройки на заданный алгоритм функционирования путем изменения своей внутренней структуры. Построенные на основе ПЛИС устройства характеризуются высокой скоростью работы, низкой стоимостью и малыми сроками проектирования.
 |
Лекция 5
 КОМБИНАЦИОННЫЕ СХЕМЫ
КОМБИНАЦИОННЫЕ СХЕМЫ
Комбинационными называются такие цифровые схемы, выходные сигналы которых в каждый момент времени определяются совокупностью входных сигналов и не зависят от их предыдущих состояний. В комбинационных схемах (КС) нет памяти, которая могла бы содержать ранее полученную информацию. Их работа полностью определяется таблицами истинности и описывается с помощью структурных формул.
5.1. Анализ и синтез комбинационных схем
В теории комбинационных схем рассматриваются две основные задачи: задача анализа и задача синтеза.
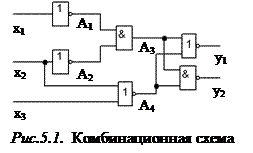 Анализ КС. Задача анализа КС может быть сформулирована как задача нахождения структурной формулы, описывающей работу заданной схемы.
Анализ КС. Задача анализа КС может быть сформулирована как задача нахождения структурной формулы, описывающей работу заданной схемы.
При решении этой задачи устанавливается однозначное соответствие между логическими элементами КС и ее математическим описанием.
С решением задачи анализа ознакомимся на примере КС, приведенной на рис. 5.1. Непосредственно из схемы имеем
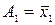 ,
, 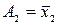 ,
, 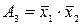 ,
,
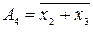 ,
, 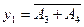
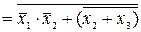 ,
,
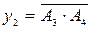
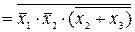 .
.
Как видно из приведенного примера, анализ КС не вызывает принципиальных затруднений.
Синтез КС. Задача синтеза может быть сформулирована как задача построения цифрового устройства, реализующего заданную булеву функцию в заданном базисе логических элементов.
Синтез КС производится в несколько этапов. На первом этапе составляют аналитическое описание (систему структурных формул в СДНФ или в СКНФ) заданных, как правило, таблично булевых функций. На втором этапе минимизируют полученные структурные формулы и осуществляют переход в заданный базис. При этом при переходе в базис И-НЕ обычно используют структурные формулы в СДНФ, а при переходе в базис ИЛИ-НЕ – структурные формулы в СКНФ.
На заключительном этапе синтеза осуществляют переход от минимизированных структурных формул к структурной схеме КС.
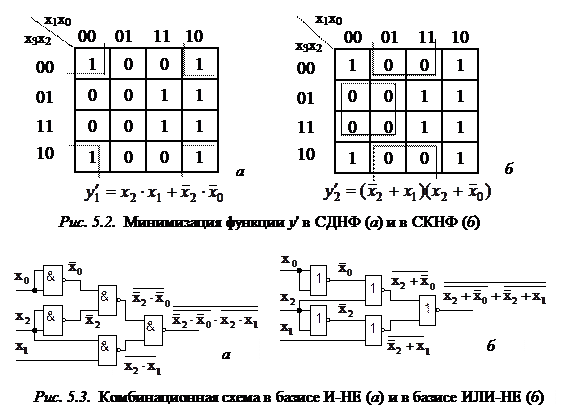
В качестве примера рассмотрим синтез КС, реализующей функцию у ', заданную таблично (табл. 5.1). На первом этапе синтеза получим структурную формулу функции у' в СДНФ
y '1= 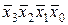 +
+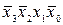 +
+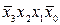 +
+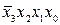 +
+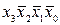 +
+
+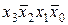 +
+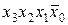 +
+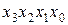 (5.1)
(5.1)
и структурную формулу этой же функции в СКНФ
y '2 = 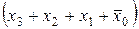 ∙
∙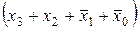 ∙
∙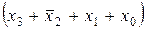 х
х
х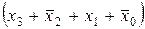 ∙
∙ ∙
∙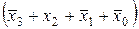 х
х
х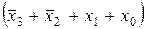 ∙
∙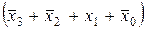 . (5.2)
. (5.2)
5.2. Сумматоры и вычитатели
Сложение является основной арифметической операцией, выполняемой в цифровых устройствах. Другие арифметические операции – вычитание, умножение, деление – сводятся к сложению. КС, выполняющие операцию «сложение», называются сумматорами. Применяются одноразрядные и многоразрядные сумматоры.
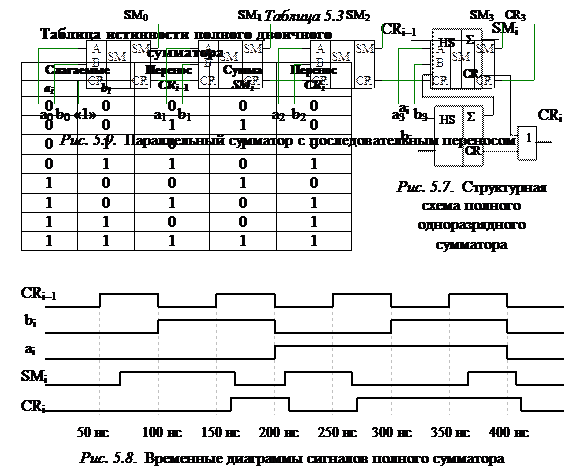
 Одноразрядные двоичные сумматоры. Одноразрядные двоичные сумматоры могут быть полными и неполными. Неполный двоичный сумматор (полусумматор) предназначен для сложения двух одноразрядных двоичных чисел. Составленные в соответствии с таблицей истинности полусумматора (табл. 5.2) структурные формулы булевых функций SM и CR имеют вид:
Одноразрядные двоичные сумматоры. Одноразрядные двоичные сумматоры могут быть полными и неполными. Неполный двоичный сумматор (полусумматор) предназначен для сложения двух одноразрядных двоичных чисел. Составленные в соответствии с таблицей истинности полусумматора (табл. 5.2) структурные формулы булевых функций SM и CR имеют вид:
SM = 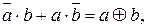 CR =
CR = 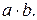 (5.5)
(5.5)

Условное обозначение полусумматора и его структурная схема приведены на рис. 5.4. Временные диаграммы сигналов полусумматора, реализованного на ИС КР1533, приведены на рис. 5.5. Из них видно, что выходные сигналы полусумматора формируются с задержкой относительно его входных сигналов.

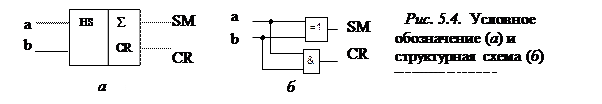
|
|
Составленные в соответствии с табл. 5.3 структурные формулы булевых функций SMi и CRi полного двоичного сумматора в СДНФ имеют вид:
SMi = ai bi CRi– 1 + 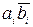
 i –1 +
i –1 +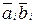 CRi– 1 +
CRi– 1 +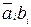
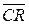 i –1,
i –1,
CRi = ai bi CRi– 1 + ai bi 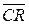 i –1 +
i –1 + 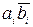 CRi– 1 +
CRi– 1 +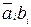 CRi– 1. (5.6)
CRi– 1. (5.6)
Можно различным образом преобразовать выражения (5.6) и получить много различных вариантов реализации функций суммы и переноса. Например, выражения
SMi = ai  bi
bi  CRi– 1,
CRi– 1,
CRi = ai·bi + CRi– 1 (ai Å bi) (5.7)
показывают возможность реализации полного одноразрядного сумматора на двух полусумматорах и логическом элементе ИЛИ (рис. 5.7). Временные диаграммы сигналов такого сумматора, реализованного на ИС КР1533, приведены на рис. 5.8.
 |
Параллельные многоразрядные сумматоры. Параллельные многоразрядные сумматоры состоят из группы одноразрядных сумматоров, число которых определяется разрядностью суммируемых чисел. Простейшими из параллельных сумматоров являются сумматоры с последовательным переносом (рис. 5.9). Сложение многоразрядных чисел в подобных сумматорах предусматривает одновременную подачу всех разрядов слагаемых, а процесс суммирования осуществляется последовательно, так как сигнал суммы в каждом разряде сумматора может быть сформирован лишь при наличии сигнала переноса из предыдущего разряда.
Реализация параллельных сумматоров с последовательным переносом не вызывает затруднений, однако быстродействие их невелико. Более высокое быстродействие обеспечивают параллельные сумматоры со сквозным переносом.
Дальнейшее увеличение быстродействия имеет место в сумматорах с ускоренным переносом, в которых операция сложения выполняется как поразрядная операция и на распространение сигнала переноса дополнительное время не требуется. В таких сумматорах сигнал переноса в каждом разряде формируется одновременно с поступлением сигнала переноса в младший разряд.
Вычитатели двоичных чисел. Операцию вычитания двоичного числа B = bn –1 bn –2 ... b 1 b 0 из числа A = an –1 an –2 ... a 1 a 0 можно выполнить с помощью многоразрядного вычитающего устройства, построенного на одноразрядных полных вычитателях.
Однако более предпочтительным является устройство, в котором арифметические операции сложения и вычитания выполнены на полных сумматорах. Принципиальная возможность построения такого устройства основана на возможности замены операции арифметического вычитания операцией алгебраического сложения чисел, представленных в дополнительном или в обратном коде.
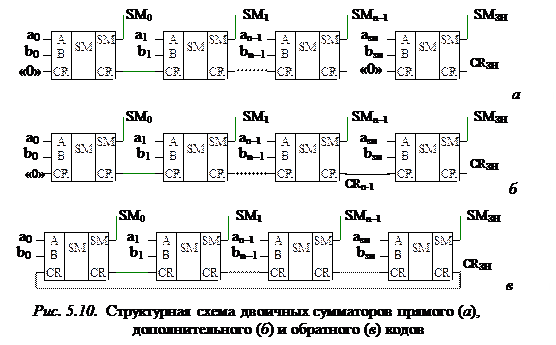 |
В общем случае в зависимости от используемого для представления двоичных чисел кода различают многоразрядные сумматоры прямого кода, дополнительного кода и обратного кода (рис. 5.10).
Двоичный сумматор прямого кода можно использовать для сложения чисел, имеющих одинаковые знаки. Характерной особенностью такого сумматора является отсутствие поразрядного переноса между старшим значащим и знаковым разрядами (рис. 5.10, а).
Двоичный сумматор с цепью поразрядного переноса из старшего значащего разряда в знаковый (рис. 5.10, б) является двоичным сумматором дополнительного кода. Он выполняет алгебраическое сложение двоичных чисел, представленных в дополнительном коде.
Алгебраическое сложение двоичных чисел, представленных в обратном коде, осуществляет двоичный сумматор обратного кода. Характерной особенностью такого сумматора является наличие не только цепи поразрядного переноса из старшего значащего разряда в знаковый разряд, но и цепи циклического переноса из знакового разряда в младший значащий разряд (рис. 5.10, в).
Сложение и вычитание десятичных чисел, представленных в коде 8-4-2-1. Сложение десятичных чисел, представленных в двоично-десятичном коде, выполняется, как правило, в рамках каждого десятичного разряда, т. е. в рамках каждой тетрады. Сумматор для одной тетрады представляет собой устройство, которое имеет 8 входов для ввода двоичных символов ai ', bi ', ci ', di ' и ai '', bi '', ci '', di '',образующих десятичные разряды слагаемых, и один вход для сигнала десятичного переноса из младшей тетрады. Такой сумматор имеет 4 выхода суммы SM 0, SM 1, SM 2, SM 3 и выход десятичного переноса в старшую тетраду.
При реализации подобных суммирующих устройств на основе двоичных сумматоров возникают определенные трудности, обусловленные необходимостью вырабатывать десятичный перенос и производить коррекцию результата, из-за того, что тетрада реализует 16 различных комбинаций, а в любом двоично-десятичном коде используется только десять.
Большинство микропроцессоров и микроконтроллеров содержат программно-управляемые средства выполнения десятичной коррекции. Они осуществляют коррекцию результата сложения двоичным сумматором десятичных чисел, представленных в двоично-десятичном коде 8-4-2-1, когда при сложении получаются недопустимые комбинации (1010,…,1111) или формируется перенос из младшей тетрады в следующую старшую. Коррекция полученного при сложении результата осуществляется путем прибавления к нему числа 610 = 01102, причем возникающие в процессе коррекции переносы учитываются.
5.3. Схемы сравнения двоичных чисел
В цифровых устройствах наибольшее распространение получили два способа сравнения двоичных чисел А и В, устанавливающих факт их равенства.
Первый способ заключается в вычитании одного числа из другого и определении по полученной разности равенства или неравенства сравниваемых чисел. Этот способ нашел широкое применение в микропроцессорах и микроконтроллерах.
Операция сравнения может выполняться также с помощью комбинационной схемы, формирующей соответствующий сигнал только в случае совпадения цифр во всех разрядах сравниваемых чисел.
Для установления равенства одноразрядных двоичных чисел можно воспользоваться функцией «эквивалентность»
Ri = 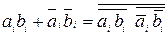 (5.8)
(5.8)
или функцией «отрицание неравнозначности»
Ri = 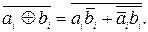 (5.9)
(5.9)

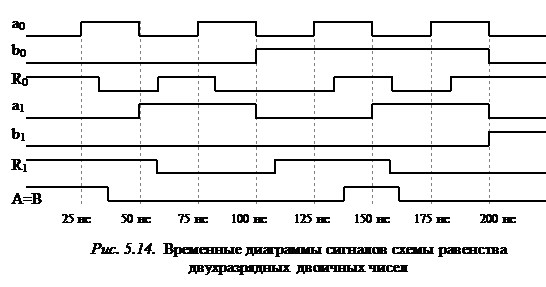
На рис. 5.11 приведены различные варианты реализации схем равенства одноразрядных двоичных чисел и изображено их условное обозначение. Временные диаграммы сигналов схемы равенства кодов (рис. 5.11, в), реализованной на ИС КР1533, приведены на рис. 5.12.
Для установления равенства n -разрядных двоичных чисел А и В необходимо реализовать функцию Ri для каждого их разряда, то есть
f 1(A, B) = 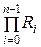
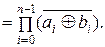 (5.10)
(5.10)
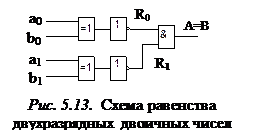
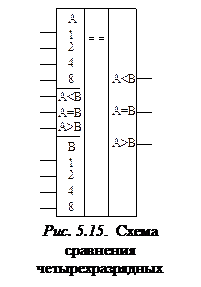
 |
Кроме рассмотренных схем применяются также комбинационные схемы, выявляющие большее или меньшее из двух сравниваемых многоразрядных двоичных чисел. Условное обозначение такой схемы сравнения двух четырехразрядных двоичных чисел приведено на рис. 5.15. Четыре пары входов используются для приема сравниваемых чисел А 3 А 2 А 1 А 0 и В 3 В 2 В 1 В 0. Входы А < B, А = B и А > B предназначены для увеличения емкости схемы сравнения (соединения нескольких ИС при сравнении чисел с разрядностью n > 4). На выходах А < B, А = B и А > B формируется логическая единица, если из двух сравниваемых чисел А и В А < В, А = В и А > В соответственно.
5.4. Преобразователи кода
 К преобразователям кода (ПК) относятся цифровые схемы, осуществляющие преобразование входных слов {
К преобразователям кода (ПК) относятся цифровые схемы, осуществляющие преобразование входных слов {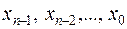 } из одного алфавита в выходные слова {
} из одного алфавита в выходные слова {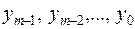 } другого алфавита. Условное графическое обозначение преобразователя двоично-десятичного кода 8-4-2-1 в двоично-десятичный код 2-4-2-1 приведено на рис. 5.16.
} другого алфавита. Условное графическое обозначение преобразователя двоично-десятичного кода 8-4-2-1 в двоично-десятичный код 2-4-2-1 приведено на рис. 5.16.
Для построения комбинационного преобразователя кода необходимо располагать таблицей истинности, в соответствии с которой синтезируется многовыходная комбинационная схема, осуществляющая преобразование кода. Синтез подобных схем производится в соответствии с правилами, изложенными ранее.
5.5. Шифраторы и дешифраторы
Шифраторы и дешифраторы являются частным случаем преобразователей кода.
 Шифратором называется преобразователь кода 1 из N в двоичный код. Дешифратор реализует обратную функцию. Он является преобразователем двоичного n -разрядного кода в код 1 из N, где N = 2 n.
Шифратором называется преобразователь кода 1 из N в двоичный код. Дешифратор реализует обратную функцию. Он является преобразователем двоичного n -разрядного кода в код 1 из N, где N = 2 n.
Шифраторы. Синтез шифратора рассмотрим на примере преобразования кода 1 из 4 в двоичный код. Правила функционирования такого шифратора приведены в табл. 5.4. Непосредственно из нее следует: y 0 = = x 1 + x 3 и y 1 = x 2 + x 3.
Схема шифратора, построенного в соответствии с этими формулами, и его условное обозначение приведены на рис. 5.17, а временные диаграммы его сигналов – на рис. 5.18.
Аналогичным образом синтезирует шифраторы кода 1 из n влюбой другой код.
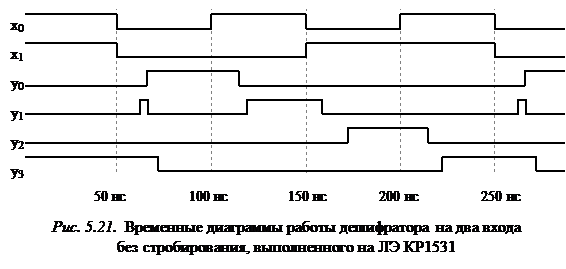
Дешифраторы. Дешифраторы по способу вывода информации подразделяются на дешифраторы со стробированием и дешифраторы без стробирования, по количеству используемых выходов – на полные и неполные.

Полный дешифратор имеет n информационных входов и  выходов. Полный дешифратор без стробирования описывается следующими структурными формулами:
выходов. Полный дешифратор без стробирования описывается следующими структурными формулами:
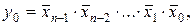
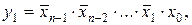
.
. (5.11)
.
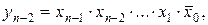
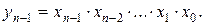
Дешифратор может быть построен непосредственно по структурным формулам (5.11) без какого-либо их логического преобразования. При этом каждая структурная формула реализуется отдельным ЛЭ И с числом входов, равным количеству входных переменных. При построении дешифратора на элементах И-НЕ на его выходах формируются не функции yi, а их инверсии.
|
Структурная схема полного дешифратора на два входа без стробирования с прямыми выходами и его условное обозначение приведены на рис. 5.19. Выходы дешифратора принято обозначать таким образом, что индекс при букве y является десятичным эквивалентом распознаваемого входного кода. Временные диаграммы работы такого дешифратора, построенного на идеальных логических элементах, не задерживающих выходные сигналы, приведены на рис. 5.20.
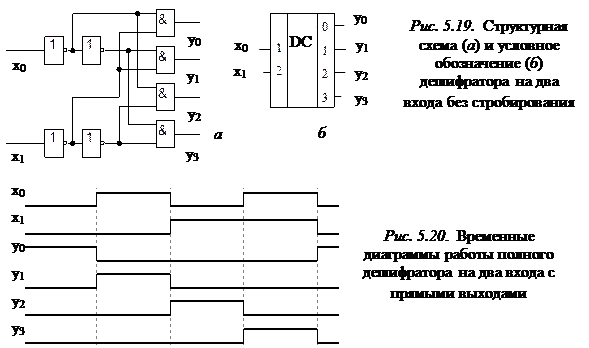
 |
Применение логических элементов с меньшими задержками распространения сигналов лишь уменьшает длительность этих помех, но не устраняет их полностью.
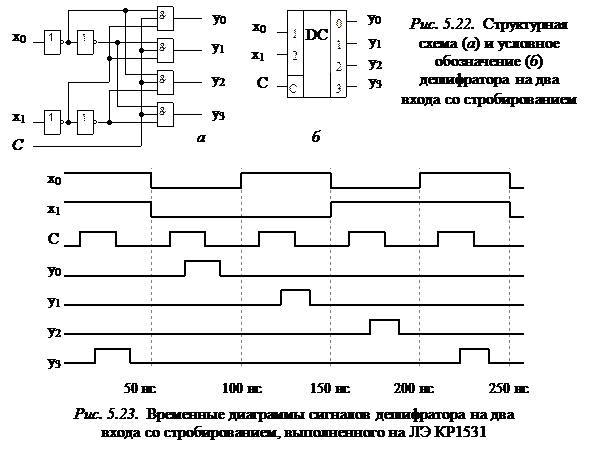
 Наличие стробирующего входа (их может быть несколько) позволяет на базе дешифраторов с числом входов n со стробированием строить дешифраторы с числом входов n + 1 без стробирования. На рис. 5.24 приведен пример построения полного дешифратора на три входа без стробирования на базе двух дешифраторов на два входа со стробированием.
Наличие стробирующего входа (их может быть несколько) позволяет на базе дешифраторов с числом входов n со стробированием строить дешифраторы с числом входов n + 1 без стробирования. На рис. 5.24 приведен пример построения полного дешифратора на три входа без стробирования на базе двух дешифраторов на два входа со стробированием.
5.6. Селекторы-мультиплексоры и демультиплексоры
Селектор-мультиплексор представляет собой устройство, имеющее n информационных входов, w адресных входов (n ≤ 2 w), один выход и предназначенное для подключения к выходу одного из информационных входов. Селектор-мультиплексор можно рассматривать как многопозиционный переключатель, значение сигнала на выходе которого определяет положение скользящего контакта (рис. 5.25). Положением его управляет сигнал выбора (комбинация сигналов на адресных входах), который указывает, какой из информационных входов должен быть соединен с выходом.
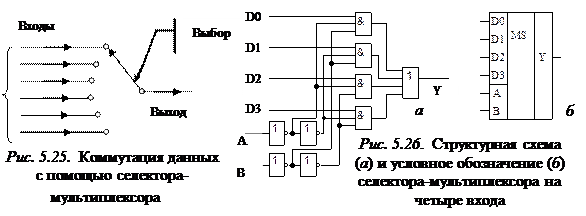 |
Схема селектора-мультиплексора на четыре входа и его условное обозначение приведены на рис. 5.26.
Если обозначить информационные сигналы буквами D 0, D 1, D 2 и D 3, адресные сигналы буквами А и В (А – младший разряд), то правило функционирования селектора-мультиплексора на четыре входа можно определить следующей структурной формулой:
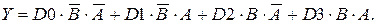 (5.12)
(5.12)
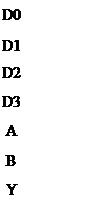 | |||
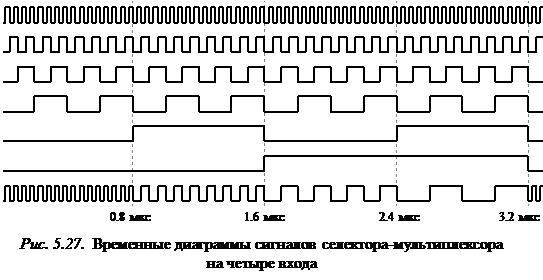 | |||
Временные диаграммы сигналов такого селектора-мультиплексора приведены на рис. 5.27.
Для расширения функциональных возможностей серийно выпускаемые селекторы-мультиплексоры наряду с адресными и информационными входами могут иметь стробирующий вход С, а также прямой и инверсный выходы.
 Демультиплексор имеет один информационный вход, w адресных входов и n (n ≤ 2 w) информационных выходов. Он предназначен для подключения информационного входа к одному из его выходов. Демультиплексор можно рассматривать как многопозиционный переключатель (рис. 5.28), в котором положение скользящего контакта определяет подключаемый к информационному входу выход. Положением этого контакта управляет сигнал выбора (комбинация сигналов на адресных входах), который указывает, какой из выходов должен быть соединен с входом.
Демультиплексор имеет один информационный вход, w адресных входов и n (n ≤ 2 w) информационных выходов. Он предназначен для подключения информационного входа к одному из его выходов. Демультиплексор можно рассматривать как многопозиционный переключатель (рис. 5.28), в котором положение скользящего контакта определяет подключаемый к информационному входу выход. Положением этого контакта управляет сигнал выбора (комбинация сигналов на адресных входах), который указывает, какой из выходов должен быть соединен с входом.
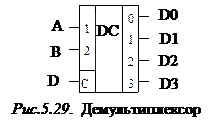 Работа демультиплексоров описывается теми же структурными формулами, которые описывают работу дешифратора со стробированием. Поэтому демультиплексор может быть реализован на базе дешифратора со стробированием, при этом стробирующий вход дешифратора играет роль информационного входа демультиплексора, а информационные входы дешифраторы – роль адресных входов демультиплексора.
Работа демультиплексоров описывается теми же структурными формулами, которые описывают работу дешифратора со стробированием. Поэтому демультиплексор может быть реализован на базе дешифратора со стробированием, при этом стробирующий вход дешифратора играет роль информационного входа демультиплексора, а информационные входы дешифраторы – роль адресных входов демультиплексора.

Поскольку демультиплексор – это тот же дешифратор, но с другим функциональным назначением, условное обозначение для него не вводится. Использование дешифратора в качестве демультиплексора иллюстрируется рис. 5.29 и рис. 5.30.
Лекция 6
ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
СХЕМЫ
К последовательностным схемам относятся цифровые устройства с памятью. Для записи правил работы последовательностных схем удобно ввести понятие «дискретное время». В соответ
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 4001; Нарушение авторских прав?; Мы поможем в написании вашей работы!