Плотнейшие шаровые упаковки в кристаллах

Симметрия структур кристаллов описывается одной из 230 федо­ровских (пространственных) групп. Причем в современной кристалло­графии широко известно важное эмпирическое наблюдение, касающе­еся неравномерного распределения структур кристаллических веществ между 230 пространственными группами. Действительно, всего девять пространственных групп описывают около 40 % всех кристаллических структур минералов и неорганических соединений, тогда как для описа­ния остальных 60 % необходима почти сотня пространственных групп. Еще 100 пространственных групп встречаются очень редко и описывают примерно 0,2 % кристаллических структур, а около 20 вообще не реали­зованы в известных к настоящему времени кристаллических структурах. Одна из наиболее успешных попыток объяснения этого факта связана с широко известной концепцией плотнейших упаковок сферических ато­мов или ионов определенного радиуса. Хотя теория плотнейших упако­вок разработана математиками, ее использование существенно упрощает симметрийный анализ и описание геометрии расположения атомов или ионов в кристаллических структурах многих веществ.

Например, в случае с ненаправленной и ненасыщаемой металличе­ской связью атомы, подчиняясь геометрическому принципу максималь­ного заполнения кристаллического пространства, располагаются в боль­шинстве случаев плотнейшим образом. Это позволяет, представив атомы в виде несжимаемых шаров одинакового размера, использовать теорию плотнейших упаковок для описания многих кристаллических структур.

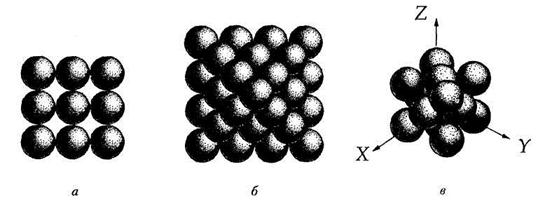
Исторически первой была замечена укладка квадратных слоев, т. е. слоев тетрагональной симметрии (рис. 7.5 а). Укладывая друг на друга эти слои так, чтобы шары каждого следующего слоя попадали в лунки между четырьмя шарами предыдущего слоя, получим максимально плот­ную упаковку шаров, т. е. будет достигнут максимальный коэффициент заполнения пространства одинаковыми шарами — 74,05 % (рис. 7.5 б). Нетрудно убедиться в том, что каждый шар в этом случае будет касаться 12 соседних шаров: четыре шара в слое, четыре сверху и четыре снизу. Такая упаковка имеет кубическую симметрию, и в выделенной в ней эле­ментарной ячейке шары будут располагаться по узлам гранецентриро-ванной решетки Браве (рис. 7.5 в).

Такой способ плотнейшей укладки шаров долгое время считался единственным, что на первый взгляд подтверждалось равенством числа шаров и лунок в каждом слое (каждый шар окружен четырьмя лунками, каждая лунка — четырьмя шарами). При этом шары каждого квадратно­го слоя заполняют все лунки предыдущего, и, казалось бы, никаких иных вариантов укладки шаров одинакового размера предложить нельзя.

 

Рис. 7.5. Плотнейшая шаровая укладка из квадратных слоев: а — изолированный квадратный шаровой слой (соотношение числа шаров и лунок — 1:1); б — квадратные слои образуют плотнейшую упаковку; в — шары плотнейшей упаковки служат узлами кубической гранецентрированной (F) решетки Браве

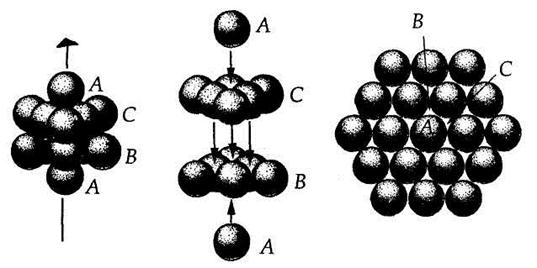
Однако, более 100 лет назад англичанин В. Барлоу сориентировал кубическую ячейку плотнейшей упаковки вдоль одной из осей 3-го по­рядка (рис.7.6 а), выделил в ней слои иной конфигурации и симметрии, расположенные перпендикулярно этой оси (рис. 7.6. б). В таких слоях каждый шар оказался окруженным не четырьмя, а шестью аналогичны­ми шарами (рис. 7.6. в). Это максимальное число (6) касаний характе­ризует плотноупакованный — плотнейший — слой, в котором шарами (кругами в двухмерном случае) заполнено приблизительно 90,7 % двух­мерного пространства. Симметрия слоя такой конфигурации оказалась гексагональной.

Каждый шар в этом слое (назовем его слоем А) (рис. 7.6. в) окружен шестью лунками, каждая из которых в свою очередь образована тремя шарами этого же слоя. Таким образом, число лунок в слое в два раза пре­вышает число шаров. Однако кристалл — это трехмерная постройка, где один плотноупакованный слой наложен на другой таким образом, что каждый шар вышележащего слоя оказывается в треугольной лунке ни­жележащего слоя. При этом не все шесть лунок предыдущего слоя А ока­жутся заполненными шарами второго слоя (В), а только половина (рас­положить шары в каждой лунке не позволит размер шаров) (рис. 7.6. в). Следует отметить, что, пока мы рассматриваем один слой, лунки В и С, по сути, не различаются, т. е. в принципе неважно, какие из них будут заполнены — В или С. В результате такого заполнения лунок получим второй слой (например, В), геометрически совершенно эквивалентный нижележащему (А).

а	б	в
Рис. 7.6. Разделение плотнейшй укладки шаров (а) на плотнейшие слои (б), перпендикулярные оси 3-го порядка гексагональной симметрии. В изолированном плотнейшем слое (в) каждый шар окружен шестью лунками (В и С), а так как каждая лунка образована тремя шарами, то соотношение числа шаров и лунок 1: 2

Однако при наложении шаров второго слоя одни лунки (1) оказыва­ются сквозными (т. е. над ними нет шаров второго слоя В), другие (2) — несквозными (прикрыты шарами второго слоя) (рис. 7.7.). Это создает два варианта наложения шаров третьего слоя. В первом случае заполне­ние несквозных лунок (2) приведет к тому, что уже третий слой располо­жится над первым, четвертый — над вторым и т. д. В результате получен­ная упаковка плотнейших слоев окажется двухслойной и запишется как чередование двух букв АВ АВAВ... — слоев А и В (рис. 7.8. б). Во втором случае если шары третьего слоя (С) укладывать в сквозные лунки (1), то повторение наступит на четвертом слое, и закономерность чередования уже трех независимых слоев в этом случае в буквенном обозначении за­пишется как ABC ABC... (рис. 7.9).

Рис. 7.7. Шары 2-го слоя заполняют лишь половину лунок предыдущего плотноупакованного слоя. При этом образуются половина сквозных (1) и половина несквозных (2) лунок

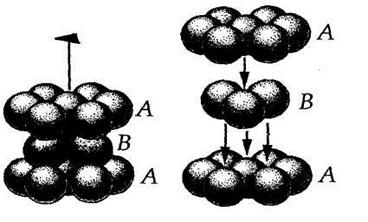
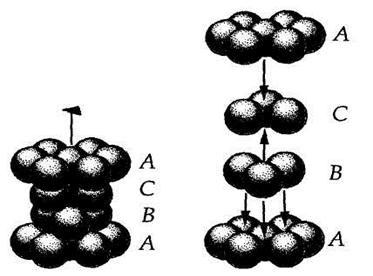
В первом случае на период повторяемости упаковки будут при­ходиться два слоя А и В (независимый пакет АВ), в результате чего возникает двухслойная плотнейшая упаковка гексагональной симмет­рии — АВ АВ АВ... (рис. 7.8). Отсюда и ее название — гексагональная плотнейшая упаковка (ГПУ). Во втором случае формируется упаковка из трех слоев А, В и С кубической симметрии (независимый пакет ABC) — кубическая плотнейшая упаковка (КПУ) — ABC ABC... (рис. 7.9). Сле­дует отметить, что если в гексагональной упаковке перпендикулярно единственному направлению осей 3-го порядка можно выделить лишь одну систему параллельных плотноупакованных слоев, то в кубической плотнейшей упаковке с четырьмя направлениями осей 3 таких систем плотнейших слоев будет четыре и каждая из них окажется перпендику­лярна одному из направлений осей 3-го порядка.

Каждый слой гексагональной упаковки расположен между одинако­выми слоями (слой А — между слоями В, слой В — между слоями А), т. е. лежит в плоскости симметрии, связывающей верхний и нижний слои. В кубической упаковке каждый слой расположен между двумя разны­ми слоями (слой А — между слоями В и С, слой В — между слоями А и С и т. д.). Таким образом, верхний и нижний соседние слои относитель­но центрального в двухслойной плотнейшей упаковке располагаются одинаково, в трехслойной упаковке они оказываются развернутыми от­носительно друг друга на 60°.

Каждый шар любой упаковки попадает в лунку, образованную тре­мя шарами предыдущего слоя, и касается 12 соседей, т. е. его коорди­национное число равно 12. Однако, несмотря на одинаковое КЧ шаров любой плотнейшей упаковки (12), координационные полиэдры в них различаются: в трехслойной кубической плотнейшей упаковке коор­динационный многогранник вокруг каждого шара имеет форму ар­химедова кубооктаэдра (рис. 7.5 и), в

а	б
Рис. 7.8. Двухслойная (гексагональная) плотнейшая упаковка – АВ АВ АВ…(а) и её разделение на слои (б)

а	б
Рис. 7.9. Двухслойная (кубическая) плотнейшая упаковка – АВС АВС АВС… (а) и её разделение на слои (б)

двухслойной гексагональной упаковке — форму гексагонального аналога кубооктаэдра (рис. 7.5 к) с единственной осью 3-го порядка. Во всех случаях коэффициент запол­нения пространства одинаков и равен 74,05 %. Различные закономерные комбинации трех слоев — А, В и С — позволяют получить бесконечное множество многослойных упаковок симметрии (например, четырех-слойную — ABAC..., шестислойную — АВСАСВ... и т. п.) с тем же мак­симальным коэффициентом заполнения пространства и координацион­ным числом каждого шара 12. При этом существенно то, что симметрия всех таким образом полученных упаковок описывается только восе­мью пространственными группами, семь из которых — гексагональные и лишь одна (трехслойная – кубическая.

В многослойной модели из одинаковых атомов-шаров, пока мы рас­сматриваем один слой, лунки 1 и 2 (см. рис. 7.7) принципиально не отличаются друг от друга. Но как только накладывается второй слой, лунки одного типа (например, 2) оказываются окруженными четырь­мя соседними шарами, а лунки другого типа (например, 1) — шестью. Теперь они оказываются совершенно разными, поскольку в плотноупакованном пространстве образуются два типа пустот: в первом случае, соединив центры тяжести четырех шаров, получим тетраэдр — тетраэдрическую пустоту (рис. 7.10 а, б), во втором получим пустоту в форме октаэдра — октаэдрическую пустоту (рис. 7.10 в,г). Это главные пустоты плотнейшей упаковки; можно говорить и о тригональных (треугольных) пустотах, расположенных в самом плотноупакованном слое (рис. 7.10 д), и несколько условно — о позициях с КЧ = 2 (рис. 7.10 е). Перечисленные пустоты в конкретных кристаллических структурах могут быть заняты более мелкими атомами, обычно катионами. Таким образом, все много­образие кристаллических структур, построенных на основе плотнейших упаковок, связано с геометрией заполнения пустот того или иного типа.

а	б	в
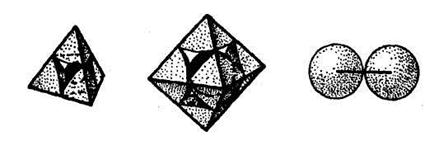
г	д	е
Рис. 7.10. Типы пустот в плотнейших упаковках: а, б — тетраэдрическая; в, г — октаэдрическая; д — тригональная; в — двухкоординатная

Дата добавления: 2014-01-07