Силы, действующие на дислокацию

Движение дислокации вызывает пластическую деформацию кристалла, т.е. дислокация совершает работу. Учитывая это, можно оперировать представлением о действии некоторой силы на линию дислокации как на самостоятельный физический объект. Фактически же дислокация - не частица, не тело, а особая конфигурация в расположении атомов. Следовательно, ниже речь идет о силе, действующей на эту конфигурацию, и такую силу не следует смешивать с силами, действующими на атомы. Это наглядно видно из рассмотрения атомного механизма перемеще­ния винтовой дислокации на рис. 9.11. Выше уже отмечалось, что в области ядра дислокации атомы смещаются вниз и вверх в направлении действующих на них сил, а сама конфигурация называемая винтовой дислокацией, перемешается вправо перпен­дикулярно этому направлению. В рассматриваемом случае можно говорить о силе, действующей на дислокацию и направленной перпендикулярно приложенным касательным напряжениям.

В общем случае на дислокацию действуют силы разного про­исхождения: внешние силы, приложенные к поверхности кристалла, внутренние силы от действия поля напряжений вокруг соседних дислокаций, инородных атомов и других несовершенств.

Ниже рассматривается случай действия только внешних сил (внутренние напряжения от других дефектов отсутствуют). Основ­ная идея расчета состоит в следующем. Кристалл от внешнего источника получает дополнительную энергию в виде механической работы А. Вся эта энергия переходит в работу Ад, совершаемую силой Fд, действующей на дислокацию (Ад=А).

Рассмотрим краевую дислокацию на рис. 11.1 и 11.2. Однородные касательные напряжения τ от внешней силы F, совершив сквозной сдвиг верхней части кристалла относительно нижней на вели­чину b, произведут работу A=Fb. Так как касательные напря­жения действуют нa площади l₁l₂ где 1₁—длина и l₂—ширина кристалла, то сила, действующая в этой плоскости, F= τl₁l₂ и A=bτl₁l₂.

Нашей целью является вычисление силы f, действующей на единицу длины дислокации. Сила, действующая на всю дислока­цию, Fд=f l₂.

При перемещении дислокации через всю длину кристалла l₁ работа этой силы Aд=Fдl₁=f l₁l₂. Она, как уже указывалось, равна затраченной работе А.

Следовательно, fl₁l₂=bτl₁l_2.Откуда

f =bτ. (11.8)

   

Рис.11.1. Сдвиг, создавший краевую дислокацию А В. Стрелка — вектор сдвига (l₁ и l₂— длина и ширина кристалла соответственно)

 

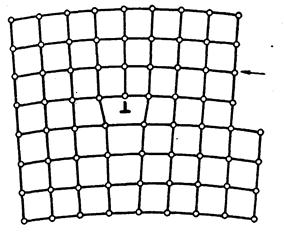
Рис. 11.2. Краевая дислокация в примитивной кубической решетке: cтрелка — вектор сдвига

Сила, действующая на единицу длины дислокации, равна про­изведению вектора Бюргерса на касательное напряжение в плос­кости скольжения. Эта сила перпендикулярна линии дислокации и направлена к той части плоскости скольжения, где скольжение еще не происходило.

Аналогичные расчеты легко выполнить для случая движения винтовой дислокации под действием однородных касательных напряжений. Здесь на сквозной сдвиг величиной b,через всю ширину кристалла l₂ затрачивается работа внешних сил А=Fb=bτl₁l_2. На линию винтовой дислокации действует пер­пендикулярная ей сила Fд=f l₁. Работа этой силы при продвижении дислокации через всю ширину кристалла Ад=Fдl_1. Так как А=Ад, то fl₁l₂=l₁l₂ и f=b.

Доказывается, что и в случае смешанной дислокации сила, действующая на единицу ее длины, равна произведению вектора. Бюргерса на касательное напряжение и направлена перпендику­лярно линии дислокации в любой ее точке в сторону участка плоскости скольжения, еще не охваченного сдвигом. Так как вектор Бюргерса является инвариантом дислокации, а при однородных касательных напряжениях величина τ на всей плоскости скольжения одна и та же, то сила, действующая на единицу длины дислокации, по своей величине (но не по направлению) одна и та же в любом участке криволинейной дислокации, нахо­дящейся в плоскости скольжения.

Если направление приложенных касательных напряжений не совпадает с направлением вектора Бюргерса, то в формуле (11.8) величина τ представляет собой проекцию касательного напряже­ния на направление вектора Бюргерса.

Когда разные участки дислокации лежат в не параллельных плоскостях, то проекция касательного напряжения на направле­ние вектора Бюргерса в разных плоскостях может быть неодина­ковой и соответственно разной будет сила f.

Например, сила, действующая на единицу длины дислокации в плоскости (111), в общем случае должна отли­чаться от силы, действующей в плоскости (111).

Весьма важно выгибание линии дислокации под действием касательных напряжений. Выгибанию дислокации препятствует ее линейное натяжение. Найдем напряжение τ, необходимое для выгибания линии дислокации в дугу с радиусом r (рис. 11.3).

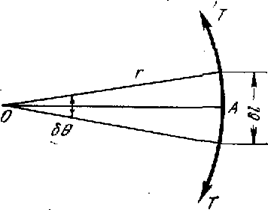
Рис. 11.3. Схема к расчету напряжения, выгибаю­щего дислокацию в дугу

На элемент дуги δl действует сила от внешних напряжений bτδl, направленная вдоль ОА. Противодействующая ей восстанав­ливающая сила F (результат линейного натяжения) направлена к центру кривизны вдоль АО. Силу F можно определить, считая, что линейное натяжение создается силами Т, приложенными по концам дуги. Тогда F = 2Tsin ¹/₂.

При малых углах sin¹/₂δθ≈¹/₂δθ и F=T δθ. Так как δθ=δl/r, то F=Tδl/r. Подставляя сюда значение Т из выражения (3), получаем для восстанавливающей силы

F=αGb²δl/r. (11.9)

Для стабильной дуги bτδ1 = F, т. е. bτδl =αGb²δl/r. Отсюда напряжение, необходимое для изгиба линии дислокации в дугу с радиусом r:

τ=αGb/r. (11.10)

Дата добавления: 2014-01-07