Упругое взаимодействие параллельных краевых дислокаций

Вокруг дислокации решетка деформирована и имеется поле напряжений, которое является источником силы, действующей на соседнюю дислокацию. Так же как и в случае действия внешних сил, приложенных к поверхности кристалла, внутренние напряже­ния от одной дислокации обусловливают наличие силы, действую­щей на единицу длины другой дислокации и равной произведениювектора Бюргерса на составляющую касательного напряжения в направлении этого вектора.

Пользуясь формулами теории упругости изотропных сред, можно определить напряжения в любой точке вокруг дислокации и рассчитать силу действия этой дислокации на другую. К упру­гому взаимодействию дислокаций применим третий закон Нью­тона: сила действия дислокации А на дислокацию Б равна и про­тивоположна по знаку силе действия дислокации Б на дислокацию А.

Поле на­пряжений вокруг краевой дис­локации не обладает такой простой симметрией, как поле напряжений вокруг винтовой дислокации. С одной стороны от плоскости скольжения име­ется область гидростатического (всестороннего) сжатия, а с другой стороны - статического растяже­ния.

Для анализа сил взаимо­действия дислокаций наиболее важны касательные напряже­ния, действующие в плоскости скольжения.

В поле напряжений вокруг краевой дислокации в точке с коор­динатами х и у касательное напряжение в плоскости, параллель­ной плоскости скольжения:

τ = [Gb/2π(1-μ)][x(x²-y²)/(x²+y²)²], (11.11)

где х—координата в направлении вектора Бюргерса; у—коорди­ната в направлении, перпендикулярном плоскости скольжения; G—модуль сдвига; μ—коэффициент Пуассона; b—вектор Бюр­герса.

Рассмотрим вначале две дислокации одного знака, расположен­ные в параллельных плоскостях скольжения (рис. 11.4,а). Начало координат поместим в точку О и будем рассматривать силу воз­действия первой дислокации в точке О на вторую дислокацию, имеющую координаты х, у в параллельной плоскости скольжения. Учитывая, что сила, действующая на единицу длины второй дислокации, f=bτ, а также выражение (11.11) для τ, можно запи­сать для силы взаимодействия параллельных краевых дислокаций одного знака:

f = [Gb²/2π (1-μ)] [x (x²-y²) / (x²+y²)²] (11.12)

Сложный характер зависимости этой силы от х обусловлен отмеченной выше асимметрией поля напряжений вокруг краевой дислокации. Эта зависимость изображается кривой на рис. 11.4, построенной в координатах f—х. Началом координат для этой кривой является точка A, от которой вверх отложены значения +f, соответствующие притяжению. Вправо от точки A отложено рас­стояние между дислокациями в направлении скольжения. Таким образом, па рис. 11.4, а совмещены две схемы: одна показывает расположение одноименных краевых дислокаций в параллельных плоскостях скольжения, находящихся на расстоянии у одна от другой, а другая — зависимость силы взаимодействия этих дисло­каций (f) от расстояния между ними в направлении скольжения (х). За единицу длины в направлении х принята величина у.

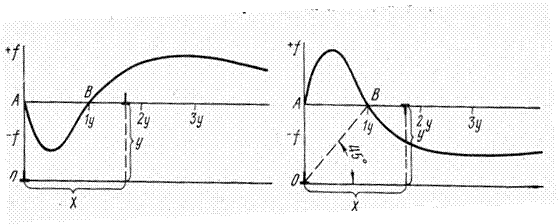
Рис. 11.4 Силы отталкивания (+f) и притяжения (-f) краевых дислокаций в параллельных плоскостях скольжения: а — одноименные дислокации; б—разноименные дислокации; х—расстояние между дислокациями в направлении плоскости скольжения; у — расстояние между плоскостями скольжения

В точке В х=у и f=0 (рис. 11.4,а). Правее точки В х> у и f>0, т. е. одноименные дислокации взаимно отталкиваются. Левее точки В х<у и f<0, т. е. одноименные краевые дислокации на относительно близких расстояниях взаимно притягиваются. Это притяжение - результат низкой симметрии поля напряжений вокруг краевой дислокации, результат внецентренного взаимодействия. Сила взаимодействия одноименных дислокаций равна нулю при х =0 (в точке A) и при х=у (в точке В). Но в точке В равновесие неустойчиво, так как не­большие отклонения от нес вправо или влево приводят к возник­новению силы, стремящейся удалить дислокацию от точки В. В точке A равновесие устойчиво: небольшие отклонения от точки A приводят к возникновению силы, стремящейся вернуть дислока­цию в эту точку (левее точки А на рис. 11.4, а должна быть кар­тина, симметричная той, что изображена правее этой точки). Таким образом, краевые дислокации одного знака, расположен­ные одна над другой, механически устойчивая конфигурация. Обусловлено это тем, что под областью растяжения от одной дислокации находится область сжатия от другой дислокации.

Когда много одноименных дислокаций распо­лагается одна под другой, такую устойчивую конфигурацию назы­вают дислокационной стенкой.

Если одноименные дислокации находятся в одной плоскости скольжения, т. е. у = 0, то формула для силы их взаимодействия приобретает следующий вид:

f=[Gb²/2π(1-μ)]x^-1. (11.13)

Следовательно, между одноименными дислокациями, находя­щимися в одной плоскости скольжения, действует только сила взаимного отталкивания, обратно пропорциональная расстоянию между ними. Отсутствие взаимного притяжения в этом случае легко понять, так как при сближении двух экстраплоскостей чрезвычайно сильно искажается решетка, возрастает энергия.

Перейдем к рассмотрению взаимодействия разноименных крае­вых дислокаций в параллельных плоскостях скольжения (рис. 11.4, б). Сила воздействия дислокации, помещенной в точке О, на дислокацию противоположного знака с координатами x, у определяется следующей формулой:

f=-[Gb²/2π(1-μ)]x (х (х² - y²)/(х² + y²)²]. (11.14)

Это выражение отличается от рассмотренного ранее для силы взаимодействия одноименных дислокаций только знаком минус.

При х > у f < 0, т. е. разноименные дислокации взаимно при­тягиваются. При х<у f > 0, т. е. они взаимно отталкиваются. При x=0 и х=у f=0. В точке A равновесие неустойчиво, так как небольшое отклонение от этой точки вызывает появление силы, стремящейся удалить одну дислокацию от другой. В точке и (x=у) равновесие устойчиво; отклонение вправо и влево от точки В вызывает появление силы, стремящейся возвратить дисло­кацию в эту точку. Таким образом, линия, соединяющая разно­именные дислокации, образующие устойчивую конфигурацию, на­ходится под углом 6° к плоскости скольжения. Если разноимен­ные краевые дислокации находятся в одной плоскости скольжения (y=0), то между ними действует только сила взаимного притя­жения, обратно пропорциональная расстоянию между дислока­циями:

f = -[Gb²/2 π (1 - μ)] x^-1 (11.15)

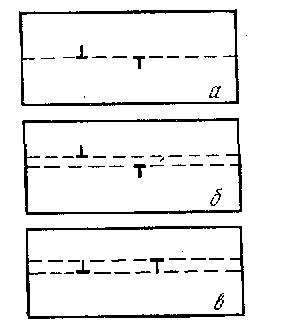
Рис. 11.5 Разноименные краевые дислокации в одной (а) и соседних (б, в) плоскостях скольжения

Когда сближающиеся в одной плоскости скольжения (рис. 11.4) дислокации разного знака подходят вплотную одна к другой, они взаимно уничтожаются. Такую аннигиляцию легко себе представить: две экстраплоскости сливаются в единую полную атомную плоскость. Если же разноименные дислокации нахо­дятся не в одной плоскости скольжения, а в соседних плоскостях, разделенных одним межатомным расстоянием (рис. 11.5,6 и в), то после их сближения образуется цепочка вакансий (б) между кромками экстраплоскостей или цепочка межузельных атомов (а), оказавшаяся «лишней» при слиянии экстраплоскостей в одну полную плоскость. При увеличении расстояния между плоскостями скольжения притяжение разноименных дислокаций переходит в рассмотренное выше взаимное отталкивание на коротких расстояниях вдоль плоскости скольжения.

Дата добавления: 2014-01-07