Пересечение растянутых дислокаций

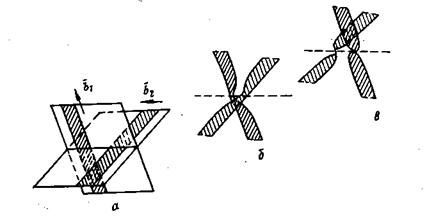
Перед моментом пересечения растянутых дислокаций их голов­ные частичные дислокации из-за упругого взаимодействия проги­баются назад в сторону хвостовых частичных дислокаций (ср. рис. 13.8, и, б). К моменту пересечения на обеих дислокациях воз­никают перетяжки дефектов упаковки и сразу же после своего образования пороги являются единичными дислокациями (рис. 13.8, в). В металлах с низкой энергией дефекта упаковки, т.е. большой шириной растянутых дислокаций, для их пересе­чения требуются повышенные напряжения.

После образования порога энергия может понизиться в резуль­тате его диссоциации, Допустим, что в плоскости АВС находится растянутая дислокация с вектором Бюргерса АС, состоящая из двух частичных дислокаций с векторами Бюргерса Аδ и δС. Эту дислокацию могут пересекать дислокации, скользя­щие в плоскостях АВС, СОВ и ADВ с векторами Бюргерса АD, СD и ВD. Как было отмечено, направление порога на дис­локации совпадает с направлением вектора Бюргерса пересе­кающей дислокации. Следовательно, на расщепленной дислокации ЛС могут образоваться нерасщепленные пороги, линии которых на­ходятся вдоль направлений АD, СD -и ВD.

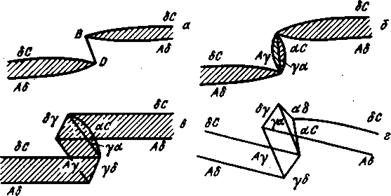
Рассмотрим порог, лежащий вдоль ВD (рис. 13.9, а). Поскольку он образовался на дислокации с вектором Бюргерса АС, то и сам порог вдоль линии ВD будет иметь вектор Бюргерса АС. Здесь уместно напомнить, что отрезки АС, ВD, Аδ, δС и др. в тетраэдре Томпсона являются векторами Бюргерса единичных и частичных дислокаций; линии же самих дислокаций могут и совпадать с на­правлениями соответствующих отрезков в тетраэдре и распола­гаться под произвольными углами к ним.

Порог с вектором Бюргерса АС может понизить свою энергию по реакции, аналогичной реакции (76): АС=А γ +γα + α С.

Рис. 13.8 Пересечение растянутых дислокаций: а — растянутые дислокации до пересечения (векторы Бюргерса b1и b2, относятся к соответствующим нерасщепленным дислокациям); б—образование перетяжек де­фектов упаковки перед пересечением; в — дислокации с нерасщепленными порогами после пересечения

Это значит, что порог — отрезок дислокации вдоль линии ВD — как бы «выбрасывает» в плоскостях АDВ и DВС частичные дис­локации Шокли с векторами Бюргерса Аγ и αС, образуя дефект упаковки в виде двугранного угла. В вершине этого угла, т. е. на линии бывшего нерасщепленного порога, возникает краевая вершинная дислокация с вектором Бюргерса γα. Вид дислокации с диссоциировавшим порогом показан на рис.9,б. Здесь и да­лее предполагается, что узлы встречи порога и дислокации стя­нуты.

Растянутый порог на рис. 13.9,6 может еще существенно понизить свою энергию по следующей реакции:

Аδ +Аγ = δγ.

Здесь образовалась новая вершинная дислокация δγ в результате взаимодействия одной дислокации Шокли, принад­лежащей исходной растянутой дислокации, и одной дислокации Шокли, принадлежащей расщепленному порогу. Соответствующая конфигурация дислокации с расщепленным порогом показана на рис. 13.9,в.

Кроме только что указанной реакции, возможна аналогичная ей реакция образования еще одной вершинной дислокации: αС + δС = αδ. Эта реакция также приводит к существенному пони­жению энергии.

На рис. 13.9, и показан окончательный вид растянутой дислока­ции с порогом, который после своего образования расщепился, претерпев ряд реакций, и получил сложную форму. Рассмотрен­ное расщепление порога привело к сильному снижению его энер­гии.

Рис. 13.9 Стадии расщепления порога ВО на дислокации в г. ц. к. решетке

Скольжение порога возможно только в том случае, если он под действием приложенных напряжений стянется в отрезок единичной дислокации. Чем больше снижается энергия при диссоциации порога, тем больше придется затратить энергии на его стягивание. Если приложенные напряжения недостаточно велики, то порог остается расщепленным. Такой порог, не может скользить и сильно тормозит движение дислокации.

В заключение следует отметить, что роль порогов в поведении дислокаций и образовании точечных дефектов необычайно велика. Поведение же порогов, особенно расщепленных, довольно сложное и изучено слабо.

Контрольные вопросы

1. Объясните, что нужно для того, чтобы произошло поперечное скольжение растянутых дислокаций.

2. Запишите стадии поперечного скольжения растянутых дислокаций.

3. Объясните, как происходит перестройка кристаллической решетки при двойниковании, где образуется линия двойникующей дислокации.

4. Дайте понятие сверхструктурной дислокации.

5. Объясните, что называют парной дислокацией в кристалле со сверхструктурой.

6. Опишите общие закономерности пересечения единичных дислокаций.

7. Опишите, как ведут себя пороги на дислокациях при их скольжении.

8. Покажите образование диполя и призматических петель при скольжении винтовой дислока­ции длинным порогом.

Дата добавления: 2014-01-07