Специальные и произвольные границы

Высокоугловые границы

Границы зерен, выросших из разных центров при кристаллизации и фазо­вых превращениях в твер­дом состоянии, чаще всего бывают высокоугловыми.

Высокоугловые гра­ницы — это «старейший» вид дефектов кристалли­ческого строения метал­лов, обнаруженный в са­мых ранних металлографических работах при изучении под микроскопом протравленной поверхности шлифов.

Хотя описанию границ зерен посвящена обширная литера­тура, до сих пор строгая общая теория высокоугловых границ не создана.

В начале XX столетия была выдвинута гипотеза аморфной прослойки по границам, аморфного «цемента», обеспечивающего сцепление соседних кристаллов. Но позже полученные экспери­ментальные данные о зависимости энергии границ, скорости их миграции, скорости диффузии по границам и других их характе­ристик от разницы кристаллографической ориентации зерен по обе стороны от границы пришли в противоречие с гипотезой аморфной прослойки, согласно которой такого влияния не должно быть.

В 1929 г. была предложена модель переходной решетки. В этой модели граница является слоем толщиной 1—2 атомных диаметра, в котором атомы занимают такие положения (комп­ромиссные между положениями узлов решеток соседних зерен), при которых их потенциальная энергия в пограничном слое ми­нимальна. Естественно, что и строение, и поведение границы — переходной зоны должны зависеть от разориентировки соседних зерен.

К настоящему времени достигнут значительный, прогресс в понимании атомного строения высокоугловых границ благо­даря экспериментальным исследованиям с помощью ионного проектора и электронной микроскопии, а также благодаря машинному моделированию—численным расчетам на ЭВМ энер­гетически выгодных координат атомов на границе.

Экспериментально прямо доказано, что ширина границ зе­рен в чистых металлах не превышает двух—трех атомных диа­метров.

В 1949 г. Кронберг и Вильсон ввели представление о специаль­ных границах, отвечающих некоторым особым разориснтиров-кам соседних зерен и отличающихся пониженной энергией бла­годаря более совершенному строению, чем произвольные гра­ницы (границы общего типа).

При развороте двух одинаковых решеток вокруг общей кри­сталлографической оси на определенный угол часть одной ре­шетки совпадает с узлами другой решетки. Такие совпадающие узлы, например вдоль прямой тп на рис. 5, образуют свою трехмерную «сверхрешетку» — общую для обоих зерен решетку совпадающих узлов (РСУ). Характерным дискретным углам по­ворота соответствует определенная плотность совпадающих узлов, т. е. их доля по отношению ко всем узлам решетки ме­талла- Например, на рис. 5 при угле поворота 36,9° вокруг оси <001> РСУ образована каждым пятым атомом соседних зерен, т. е. плотность совпадающих узлов равна 1/5.

Для характеристики РСУ чаще используют обратную плот­ность совпадающих узлов, обозначаемую 2, – число узлов ре­шетки метала, приходящихся на один совпадающий узел в об­щей сверхрешетке. Например, в случае, изображенном на рис. 5,2=5.

При любой разориентировке решеток соседних зерен можно найти некоторое число совпадающих узлов. Но при низкой их плотности понятие об общей сверхрешетке практически теряет смысл для анализа строения границ зерен. Обычно рассматри­вают решетки совпадающих узлов при значениях S, находя­щихся в интервале 3—25 (при S=1 угол разориентировки ра­вен нулю).

Если граница зерен располагается вдоль плоскости с мак­симальной плотностью совпадающих узлов в РСУ (см. рис. 16.5), то из-за большого числа атомов, принадлежащих одновременно решеткам соседних зерен, структура границы совпа­дающих узлов весьма совершенна и соответственно ее энергия минимальна. Такая граница является специальной. В модели РСУ плоскость специальной границы параллельна плоскостям РСУ с низкими индексами.

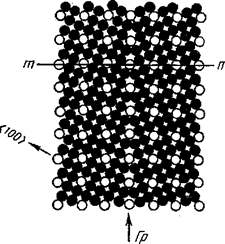Рис. 16.5 Специальная граница Гр совпадающих узлов (светлые кружки) между зернами с примитивной кубической решеткой, развернутыми на 36,0 град вокруг оси <001>

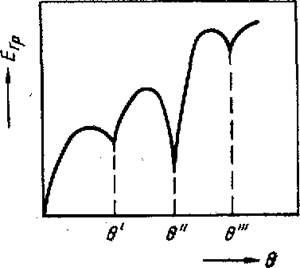Рис. 16.6 Зависимость энергии границ зерен Егр от угла их разориентировки q

С увеличением угла разориентировки соседних зерен энер­гия границы между ними проходит через минимумы (рис. 16.6), соответствующие специальным границам (при углах q',q" и q"').

Если граница зерен находится под небольшим углом к плотноупакованной плоскости в РСУ, то она может иметь ступенча­тое строение (рис. 16.7), что обеспечивает минимум энергии. При этом граница стремится расположиться большей частью своей поверхности в плоскостях с максимальной плотностью совпадающих узлов, где наиболее совершенно сопряжение ре­шеток двух зерен, минимальны энергия и ширина границы (см. участки АВ и CD на рис. 16.7). Эти плоские участки границы (фасетки) соединены ступенькой (ВС). Число ступенек на еди­нице длины границы зерен тем больше, чем сильнее ее макроскопическая ориентация отклоняется от плоскости с наибольшей плотностью совпадающих узлов.

На рис. 16.7 видно, что вдоль ступеньки ВС решетки сосед­них зерен плохо сопряжены и граница здесь шире. Таким об­разом, рассматриваемая фасетированная граница представляет собой чередование областей хорошего и плохого сопряжения решеток соседних зерен, причем плохое сопряжение сосредоточено на небольших участках (ступеньках).

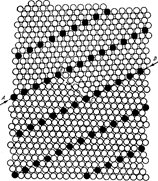
Рис. 16.7 Фасетированная ступенчатая граница ABCD между двумя зернами с о.ц.к. решеткой, развернутой на 50,5° вокруг оси <110>

В модели жестких сфер нерелаксированная идеальная гра­ница совпадающих узлов не может соответствовать минимуму энергии. На рис. 16.8 показаны физически невозможные пере­крытия жестких сфер (атомов) двух зерен справа от узлов совпадения А и В и участки отсутствия контакта зерен между этими узлами (большой избыточный объем на границе по срав­нению с совершенной решеткой внутри зерен),

Границу совпадающих узлов можно рассматривать как со­стоящую из одинаковых сегментов (АВ на рис, 16.8 или Р на рис. 16.9, а), являющихся «единицей повторяемости» двумерной периодической структуры.

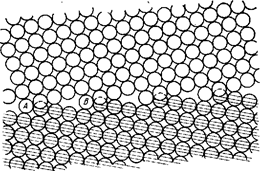
Рис. 16.8. Граница совпадающих узлов между двумя зернами (S=17)

Чтобы в пределах сегмента Р (рис. 16.9, а) уменьшить сумму энергий парных взаимодействий атомов соседних кристаллов, необходимо, как показывают расчеты, сместить кристаллы один относительно другого (без вращения), выведя границу из по­ложения совпадающих узлов (рис. 16.9,6). При такой «жесткой релаксации» каждый атом остается в узле решетки своего кристалла. Следует отметить, что хотя границы совпадающих уз­лов после указанного смещения зерен уже не существует, пе­риодичность строения границы сохраняется и сохраняется сег­мент повторяемости Р (рис, 16.9,6), равный соответствующему сегменту в идеальной границе совпадающих узлов (рис. 16.9, а).

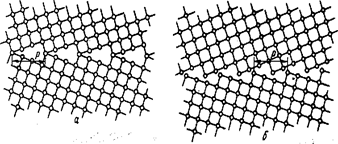
Рис. 16.9. Наклонная граница 37° <001> между зернами с кубической решеткой в по­ложении совпадения (а) и после жесткой релаксации (б)

Сумма энергий парных взаимодействий атомов в пределах каждого сегмента Р дополнительно уменьшается при индивидуальных смещениях атомов из исходных узлов так, чтобы улуч­шился контакт соседних зерен вдоль сегмента повторяемости (такая релаксация отдельных атомов на рис. 16.9, б не пока­зана). При этом по обе стороны от границы решетка должна деформироваться на расстояние, соизмеримое с длиной сег­мента Р. Избыточная энергия (в расчете на единицу площади границы) тем меньше, чем меньше сегмент повторяемости.

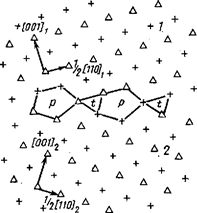
Рис. 16.10. Рассчитанная на ЭВМ струк­тура симметричной границы наклона в алюминии (S27; 31.59° [110]). Ось на­клона [110] перпендикулярна плоскости чертежа (110): 1 и 2—зерна; треугольники и кре­стики — центры атомов, соответственно, верхнего и нижнего слоя (110): р и t — многоугольники, вершины которых расположены в двух соседних слоях (110) (Саттон и Витек)

Таким образом, хотя реальная структура границ и не опи­сывается моделью совпадающих узлов, особые ориентационные соотношения решеток соседних зерен определяют малую величи­ну сегмента повторяемости в пе­риодической структуре границ и обусловливают тем самым их осо­бые свойства.

Развитие методов машинного моделирования позволило сде­лать вывод, что все без исключе­ния высокоугловые границы со­стоят из характерных струк­турных единиц — сравнительно плотноупакованных атомных группировок с определенным расположением атомов. Напри­мер, атомы внутри одной струк­турной единицы границы могут располагаться по вершинам по­лиэдров двух и более видов, со­стыкованных один с другим в определенной последовательно­сти (рис. 16.10).

Специальные границы, состоя­щие из структурных единиц од­ного типа, называют предпочти­тельными. У них очень короткий сегмент повторяемости (несколько атомных диаметров), т. е-они являются «короткопериодными». Произвольные высокоуг­ловые границы можно представить в виде повторяющегося на­бора в разной пропорции структурных единиц двух типов, т. е. они являются «длиннопериодными». С изменением угла разориентировки зерен непрерывно изменяется набор структурных единиц, из которых состоит высокоугловая граница.

Дата добавления: 2014-01-07