Сила Пайерлса

Торможение дислокаций в твердых растворах

Снука

Торможение дислокации атмосферами Коттрелла, Сузуки и

Элементов

Торможение дислокаций атомами примесей и легирующих

Перерезание дислокациями дисперсных частиц

Локальное поперечное скольжение

Выгибание дислокаций между дисперсными частицами

Торможение дислокаций дисперсными частицами

Кациями и границами зерен

Торможение дислокаций при их взаимодействии с другими дисло

План лекции

Лекция 17. Торможение дислокаций

1. Сила Пайерлса.

Скользящие дислокации всегда тормозятся, часто вплоть до полной остановки, под действием разнообразных факторов. Изучение этих факторов представляет исключительно большой интерес, так как с торможением дислокаций прямо связаны важнейшие механические свойства и прежде всего прочность • металлов.

Рассмотрим, какое минимальное (критическое) касательное на­пряжение требуется для движения краевой дислокации в кри­сталле, свободном от других дефектов.

В исходном состоянии в результате симметрии горизонталь­ные составляющие сил, действующих на атом 1 со стороны со­седей слева и справа от него, взаимно уравновешиваются. То же самое справедливо по отношению к атому, соответствующему новому (соседнему) положению дислокации. Казалось бы, что сила, необходимая для перемещения дислока­ции на одно межатомное расстояние, бесконечно мала. Однако в период перемещения дислокации в соседнее положение из-за смещений атомов симметрия межатомных сил нарушается. Чтобы дислокация преодолела потенциальный барьер, разде­ляющий два соседних се положения в энергетических ямах (точки 1 и 14 на рис. 17.1), необходима сила. Она называется силой Пайерлса (или силой Пайерлса—Набарро). Поскольку эта сила определяется свойствами решетки, то говорят о силах «трения» в решетках. Учитывая, что сила, действующая на еди­ницу длины дислокации f=bt, можно для силы Пайерлса напи­сать: f_п=bt_п, где b—вектор Бюргерса, а t_п–минимальное ка­сательное напряжение, необходимое для скольжения дислокации в совершенном кристалле (напряжение Пайерлса).

Расчет силы Пайерлса—очень сложная и до конца не ре­шенная задача. Одна из основных трудностей состоит в том, что неизвестны точное расположение атомов в ядре дислокации не точный закон изменения сил взаимодействия между соседними атомными плоскостями при сдвиге на одно межатомное рас­стояние.

Метод анализа, созданный Пайерлсом и развитый Набарро, при синусоидальном законе для силы взаимодействия соседних сдвигаемых по отношению одна к другой атомных плоскостей дает следующее выражение для напряжения Пайерлса:

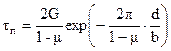(17.1)

где G—модуль упругости при сдвиге; m—коэффициент Пуас­сона; d—расстояние между соседними атомными плоскостями, в которых происходит скольжение; b — межатомное расстояние в направлении скольжения.

Чем больше силы межатомной связи, характеристикой кото­рых является модуль сдвига, тем больше t_п. Формула (17.1) качественно правильно указывает, что критическое напряжение снижается с ростом d и уменьшением b. Для пло­скостей и направлений с плотнейшей упаковкой соотношение d/b обычно наибольшее, с чем согла­суется тот факт, что скольжение легче всего идет по плоскостям и на­правлениям плотнейшей упаковки.

Рис. 17.1. Рельеф поверхности потенциальной энер­гии дислокации, обусловленной действием силы Пайерлса: А—дислокация с одним перегибом; В—дисло­кация с двумя перегибами

В кристалле, свобод­ном от других дефектов, дислокация может скользить и при напряжениях меньше напряжения Пайерлса. Благодаря действию сил Пайерлса потенциальная энергия дис­локации является периодической функцией ее положения в ре­шетке (рис. 17.2). Минимальные значения потенциальной энер­гии (канавки потенциального рельефа) соответствуют положе­ниям дислокации вдоль направлений плотнейшей упаковки. Для перемещения дислокации из одной канавки в соседнюю требуется преодолеть потенциальный барьер, приложив на­пряжение Пайерлса.

Иная картина предполагается в случае, когда одна дислока­ция расположена в соседних канавках потенциального рельефа, т. е. имеет перегибы (см. рис. 17.2). Движение перегиба вдоль линии дислокации может привести к последовательному (уча­сток за участком) переходу всей дислокации в соседнее положе­ние с минимумом энергии. Напряжение, требуемое для движе­ния перегиба параллельно направлению плотнейшей упаковки, очень мало (меньше напряжения Пайерлса). «Выбрасывание» полупетли в соседнюю канавку (образование двойного пере­гиба, см. рис. 2) происходит под действием термической акти­вации, а дальнейшее расхождение перегибов в разные сто­роны—под действием очень малых напряжений.

Скорость скольжения дислокации и, движущейся вследствие образования двойных перегибов, зависит от частоты и, соответ­ственно, энергии образования этих перегибов Un:

v=Aexp(-U_п/kT) (17.2)

Таким образом, основная идея теории дислокаций – пред­ставление о неодновременности протекания акта скольжения — распространяется и на перемещение самой линии дислокации.

Критическое касательное напряжение, обусловленное «тре­нием» в решетке, трудно не только рассчитать, но и экспери­ментально определить, так как действительный предел текуче­сти зависит не только от силы Пайерлса, но и от других фак­торов, сильно препятствующих скольжению и не связанных с действием сил Пайерлса.

Дата добавления: 2014-01-07