Примеры. Свойства отношения равномощности

Свойства отношения равномощности.

1) А~А- рефлексивность.

2) А~В, то В~А – симметричность.

3) А~В и В~С, то А~С – транзитивность.

1) n→2n, 2,4,6,… - четные натуральные

2) n→2n-1, 1,3,5,…- нечетные натуральные.

Свойства счетных множеств.

1. Бесконечные подмножества счетного множества счетны.

Доказательство. Т.к. А – счетно, то А: х₁,х₂,… - отобразили А в N.

ВÌА, В: →1, 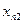→2,… - поставили каждому элементу В в соответствие натуральное число, т.е. отобразили В в N. Следовательно В – счетно. Ч.т.д.

2. Объединение конечной (счетной) системы счетных множеств – счетно.

Примеры.

1. Множество целых чисел Z – счетно, т.к. множество Z можно представить как объединение счетных множеств А и В, где А: 0,1,2,.. и В: -1,-2,-3,…

2. Множество упорядоченных пар {(m,n): m,nÎZ} (т.е. (1,3)≠(3,1)).

3 (!). Множество рациональных чисел – счетно.

Q=. Можно установить взаимно однозначное соответствие между множеством несократимых дробей Q и множеством упорядоченных пар:

. Т.о. множество Q равномощно множеству {(p,q)}Ì{(m,n)}.

Множество {(m,n)} – множество всех упорядоченных пар – счетно. Следовательно и множество {(p,q)} – счетно, а значит и Q – счетно.

Определение. Иррациональным числом называется произвольная бесконечная десятичная непериодическая дробь, т.е. g₀,g₁g₂…

Множество всех десятичных дробей образуют множество вещественных (действительных) чисел.

Множество иррациональных чисел – несчетно.

Теорема 1. Множество вещественных чисел из промежутка (0,1) – несчетное множество.

Доказательство. Допустим противное, т.е. что все числа интервала (0,1) можно занумеровать. Тогда, записывая эти числа в виде бесконечных десятичных дробей, получим последовательность:

х₁=0,а₁₁а₁₂…a_1n…

x₂=0,a₂₁a₂₂…a_2n…

…………………..

x_n=0,a_n1a_n2…a_nn…

……………………

Рассмотрим теперь вещественное число х=0,b₁b₂…b_n…, где b₁- любая цифра, отличная от а₁₁, (0 и 9), b₂ - любая цифра, отличная от а₂₂, (0 и 9),…, b_n - любая цифра, отличная от a_nn, (0 и 9).

Т.о. хÎ(0,1), но х¹x_i (i=1,…,n) т.к. в противном случае, b_i=a_ii. Пришли к противоречию. Ч.т.д.

Теорема 2. Любой промежуток вещественной оси является несчетным множеством.

Теорема 3. Множество действительных (вещественных) чисел – несчетно.

Про всякое множество, равномощное множеству вещественных чисел говорят, что оно мощности континуума (лат. continuum – непрерывное, сплошное).

Пример. Покажем, что интервал обладает мощностью континуума.

Функция у=tg x: →R отображает интервал на всю числовую прямую (график).

Дата добавления: 2014-01-07