Числа x1,x2,…,xn – члены последовательности

x_n – общий член последовательности.

Последовательность можно задать как функцию f:N→X (где Х- некоторое множество). f(n)=x_n – n-й член последовательности.

Если f:N→R, то имеем числовую последовательность.

Пример. 1) 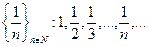; 2) ; {}: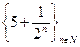

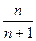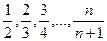
Лемма о вложенных отрезках. (Принцип Коши-Кантора)

Пусть дана некоторая последовательность отрезков числовой прямой. {I_n} [a_n;b_n].

Будем говорить, что отрезки вложены друг в друга, если I₁É I₂É… I_nÉ….

Длина отрезка - ½ I_n½.

Последовательность длин отрезка стремится к нулю, если

Лемма 1. Для любой последовательности вложенных друг в друга отрезков из R найдется точка, принадлежащая всем отрезкам последовательности.

Если последовательность длин отрезков стремится к нулю, то такая точка будет единственной (рисунок).

Доказательство. Пусть I_n=[a_n;b_n], n=1,2,… I₁É I₂É… I_nÉ…..

A={a_n} – левые концы, B={b_n}- правые концы (рисунок).

Любой левый конец меньше любого правого, т.е. .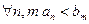

В силу свойства полноты множества R, найдется такое число с, которое разделяет левые и правые концы, т.е.

.

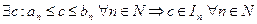Покажем единственность такой точки.

Допустим, что существует 2 точки с₁,с₂Î I_n, тогда ½ I_n½³с₂-с₁ – это противоречит тому, что длина отрезков стремится к нулю. Следовательно, существует только одна такая точка. Ч.т.д.

Лемма о предельной точке.

Пусть М – некоторое числовое множество.

Определение. Точка аÎМ называется предельной для множества М, если в любой окрестности точки а находится бесконечное множество точек из М.

Окрестностью точки х₀ называется любой интервал числовой прямой, содержащий точку х₀: V(x₀).

Симметричной окрестностью (дельта-окрестностью) точки х₀ называется интервал V(x₀,δ)=(х₀-δ;х₀+δ)={x: |x-x₀|<δ} Рисунок.

Выколотой окрестностью точки x₀ называется окрестность x₀, исключая саму эту точку: Ů(x₀,δ)={x: 0<|x-x₀|<δ}

Лемма 2. Каждое бесконечное ограниченное множество вещественной прямой имеет по крайней мере одну предельную точку.

Доказательство. Дано ограниченное бесконечное множество М, лежащее в отрезке [a;b].

Обозначим [a;b]=I₁. Разделим этот отрезок пополам. Пусть I₂ÌI₁ (I₁ÉI₂) – такая из частей, в которой содержится бесконечное множество точек из М.

I₂ делим пополам и опять выбираем ту половину, в которой содержится бесконечное множество точек из М. И.т.д. до бесконечности.

Длины отрезков ½I_n½=- стремятся к 0 (сумма геометрической прогрессии со знаменателем 0,5).

Следовательно, по лемме 1, .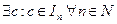

Возьмем окрестность (a;b) точки с. Если n достаточно велико, то отрезок I_n попадает в (a;b). В этой окрестности содержится бесконечное множество точек из М, т.е. с- предельная точка М. ч.т.д.

Дата добавления: 2014-01-07