Число е

Определение. Числом е называется предел последовательности x_n=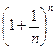, т.е.

е=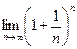

1. Покажем, что последовательность 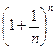- строго возрастающая.

Воспользуемся формулой бинома Ньютона:

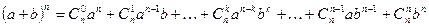
Числа 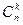, являющиеся коэффициентами в формуле бинома Ньютона, называются биномиальными коэффициентами.

Применяя эту формулу n-й член последовательности можно представить в виде:

х_n=

или

х_n=

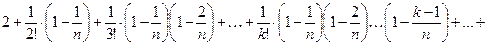
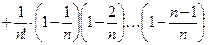(1)

Аналогично для х_n+1 члена последовательности:

х_n+1=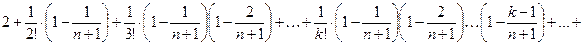

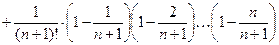(2)

Правая часть соотношения (1) содержит n слагаемых, а правая часть соотношения (2) – (n+1) слагаемых.

Сравнивая х_n и х_n+1, замечаем, что первые слагаемее в правых частях соотношений (1) и (2) одинаковы, 2-е, 3-е,…,n-е слагаемое у х_n+1 больше, чем у х_n, т.к.

; ; ….;

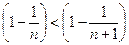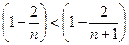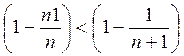
Кроме того, в составе х_n+1 есть еще (n+1)-е слагаемое, которого в составе х_n нет и которое является положительным. Следовательно, х_n<х_n+1 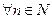, значит х_n - возрастающая.

2. Покажем, что х_n ограничена сверху. Для этого воспользуемся соотношением (1). Заменим все разности, стоящие в скобках в правой части этой формулы, на единицы, отчего правая часть увеличится (т.к. каждая разность меньше 1). Получим

х_n<2+++…++…+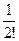

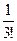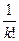Т.к. =, <,…,<,…,<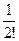

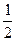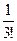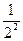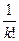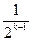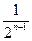
Поэтому, х_n<2+++…++…+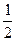

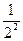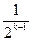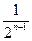
Т.к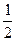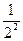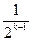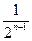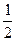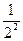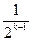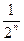. ++…++…+<++…++…++…=1,

То получаем, что х_n<2+1=3 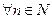, т.е. х_n ограничена сверху.

Из (1) видно, что х_n³2, следовательно 2£х_n<3 .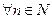

Т.к. х_n монотонна и ограничена сверху, то существует конечный 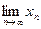, величина которого заключена между 2 и 3. Этот предел обозначается буквой е.

Натуральный логарифм.

Дата добавления: 2014-01-07