Монотонные последовательности. Определение.Последовательность {xn} называется возрастающей (неубывающей), если n=1,2, xn£xn+1

Определение. Последовательность {x_n} называется возрастающей (неубывающей), если 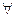n=1,2,… x_n£x_n+1

Если 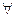n=1,2,… x_n<x_n+1, то {x_n} – строго возрастающая.

Если 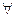n=1,2,… x_n³x_n+1, то {x_n} – убывающая (невозрастающая).

Если 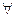n=1,2,… x_n>x_n+1, то {x_n} – строго убывающая.

Последовательности всех рассмотренных типов называются монотонными.

Примеры. 1) 1,1,0,0,…- убывающая.

2) 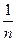: 1, 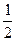, ,… - строго убывающая.

Теорема 1. 1) Если последовательность {x_n} неубывающая (в частности строго возрастающая) и ограничена сверху, то она имеет конечный предел.

2) Если последовательность {x_n} неубывающая (в частности строго возрастающая) и сверху не ограничена, то .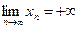

Доказательство. 1) Пусть последовательность {x_n} возрастающая, т.е. 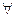n=1,2,… x_n£x_n+1

Т.к. числовое множество {x_n} ограничено сверху, то 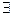С: 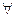n=1,2,… x_n£С

Пусть а=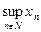- точная верхняя граница – т.к. всякое ограниченная сверху последовательность имеет точную верхнюю границу. (Покажем, что 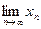=а.)

Тогда 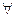n=1,2,… x_n£а (1)

Возьмем сколь угодно малое 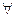e>0 и рассмотрим число а-e. Т.к. а-e<a, то по свойству супремума на множестве {x_n} найдется такой элемент 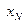, что будет >a-e.

Т.к. последовательность неубывающая, то 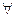n³N Þ x_n ³ 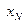(2)

Следовательно, при n³N будет x_n>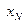>a-e (3)

При n³N будут выполняться неравенства (1) и (3), т.е.

а-e<x_n£a, а значит и а-e<x_n£a+e, т.е. 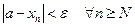. А это значит, что 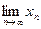=а. 2) По условию числовое множество {x_n} не ограничено сверху.

Это означает, что какое бы большое число М>0 мы ни взяли, на множестве {x_n}обязательно найдется хотя бы одни элемент 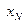такой, что 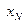>M.

Т.к. последовательность {x_n}неубывающая, то при n>N Þ x_n ³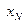, а, следовательно, при n>N будет x_n>M. А это означает, что 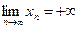. Ч.т.д.

Теорема 2. 1) Если последовательность {x_n} невозрастающая (в частности строго убывающая) и ограничена снизу, то она имеет конечный предел.

2) Если последовательность {x_n} невозрастающая (в частности строго убывающая) и снизу не ограничена, то .

(Доказательство – аналогично доказательству теоремы 1).

Доказательство. 1) Пусть последовательность {x_n} невозрастающая, т.е. 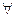n=1,2,… x_n³x_n+1

Т.к. числовое множество {x_n} ограничено снизу, то существует точная нижняя граница этого множества.

Пусть b=- точная нижняя граница. Тогда 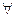n=1,2,… x_n³b (4)

Возьмем сколь угодно малое 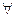e>0 и рассмотрим число b+e. Т.к. b+e>b, то по свойству инфимума на множестве {x_n} найдется такой элемент 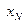, что будет <b+e.

Т.к. последовательность невозрастающая, то 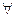n³N Þ x_n£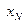

Следовательно, при n³N будет x_n£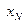<b+e (5)

При n³N будут выполняться неравенства (4) и (5), т.е.

b£x_n<b+e, а значит и b-e<x_n<b+e, т.е. 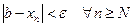. А это значит, что 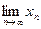=b.

2) По условию числовое множество {x_n} не ограничено снизу.

Это означает, что какое бы большое число М>0 мы ни взяли, на множестве {x_n}обязательно найдется хотя бы одни элемент 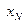такой, что 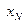<-M.

Т.к. последовательность {x_n}невозрастающая, то при n>N Þ x_n£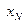, а, следовательно, при n>N будет x_n<-M. А это означает, что . Ч.т.д.

Замечание. Все утверждения теорем 1 и 2 остаются в силе и для последовательности, которая становится монотонной лишь начиная с некоторого номера, т.е. при n³N_*, N_*ÎN (т.к. без влияния на предел последовательности – любое число первых ее значений можно отбросить).

Пример. Найти 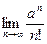(a>0).

Если 0<a<1, aⁿ – б.м. величина. Поэтому 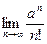=0. При а=1 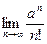==0.

Пусть a>1. В этом случае отношение 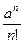представляет собой неопределенность 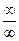. Обозначим 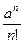=x_n. Имеем:

x_n+1=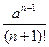=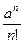×=x_n×.

Как только n+1>a (т.е. n>a-1), так последовательность x_n становится строго убывающей. Последовательность x_n ограниченна снизу (например, числом 0). Следовательно, по теореме 2 последовательность x_n имеет конечный предел. Обозначим его через с.

Для того, чтобы найти его, перейдем к пределу в равенстве

x_n+1=x_n×

Т.к. x_n+1 пробегает ту же последовательность значений, что и x_n (с точностью до первого члена), то x_n+1 имеет тот же предел с. Будем иметь:

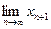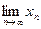=×Ûс=с×0Þс=0.

Т.о., при a>1 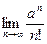=0.

Дата добавления: 2014-01-07