Введение. Тема. Производная функции одной переменной

Лекция № 9, ВАС-11, 1 сем, 2012

Тема. Производная функции одной переменной. Задача, приводящая к понятию производной, механический и геометрический смысл производной. Таблица основных формул дифференцирования.

Начиная с этой лекции и до конца учебного года, мы будем изучать дифференциальное и интегральное исчисление функции одной переменной, составляющих основу математического анализа, а также некоторые их практические приложения. Начнем с небольшой историко-биографической справки.

Элементы дифференциального и интегрального исчисления возникли уже в Древней Греции: в работе Аполлония о касательных и в трудах Архимеда о вычислении объемов. Однако по-настоящему методы математического анализа были созданы лишь в ХVII в., и их создание связано, в первую очередь, с именами величайших ученых Ньютона и Лейбница.

Исаак Ньютон (1643 – 1727) – английский математик, физик, механик, астроном. Окончил Кембриджский университет, преподавал в нем, был смотрителем, а затем директором Лондонского монетного двора, член парламента.

В его работах математика и механика переплетались самым естественным образом. Развитие методов математического анализа было обусловлено необходимостью создания аппарата для решения задач механики. Ньютоном были введены понятия флюенты (переменной величины) и флюксии (скорости ее изменения, то есть производной функции) и четко сформулированы и решены задачи нахождения флюксии по известной флюенте и флюенты по ее флюксии. Это не что иное, как основные задачи дифференциального и интегрального исчисления – нахождение производной по известной функции и функции (интеграла) по известной производной. Таким образом, Ньютон установил связь между дифференцированием и интегрированием.

Готфрид Вильгельм Лейбниц (1646 – 1716) – немецкий математик, физик, философ, изобретатель, юрист, историк. Окончил Лейпцигский университет, где изучал философию и право, в Йенском университете изучал математику. Круг его интересов необычайно широк – наука, преподавание, дипломатия, административная деятельность. Он принял участие в создании Берлинской академии наук и был ее первым президентом, способствовал открытию академии в Лейпциге, Вене и Петербурге, работал над проектом образования в России. Вот далеко не полный перечень того, что успел совершить Лейбниц за свою жизнь.

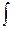Основные математические труды его посвящены разработке методов дифференциального и интегрального исчислений. Именно Лейбниц ввел символы для дифференциала и для интеграла. Им разработаны правила дифференцирования суммы, разности, произведения, частного от деления функций и многое другое. Следует отметить огромную роль Лейбница в создании современных символики и терминологии математического анализа.

Еще при жизни Ньютона и Лейбница разгорелись споры о приоритете открытия дифференциального и интегрального исчисления, не утихавшие длительное время и после их смерти. Споры, не стоившие выеденного яйца: ученые получили результаты независимо друг от друга, в различных формах, несколько раньше получил их Ньютон, но значительно позже опубликовал, оба внесли неоценимый вклад в науку.

Дата добавления: 2014-01-07