Определение понятия производной, механический смысл производной

Понятие производной, ее механический и геометрический смысл

Рассмотрим задачу, приводящую к понятию производной.

Пусть некоторое тело (например, автомобиль) движется по прямолинейному пути неравномерно по закону 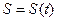. Поставим задачу определения скорости движения тела в любой момент времени. Такая скорость носит название мгновенной (истинной) скорости. Так как движение тела неравномерное, то средствами элементарной математики эту задачу решить нельзя. Для ее решения проведем следующие рассуждения (рис. 1.1).

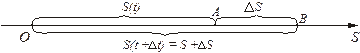Рис. 1.1

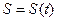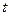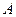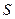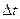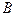Скорость тела в каждый момент времени является функцией времени, . Пусть в момент времени тело находится в точке , пройдя путь (рис. 1.1). За малый промежуток времени тело пройдет путь и окажется в точке . Средняя скорость тела на пути составит:

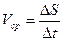. (1.1)

Эта величина не является скоростью тела в точке 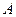, но в какой-то мере характеризует эту скорость, очевидно, тем точнее, чем меньше промежуток времени 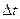. Станем неограниченно уменьшать 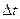, и вычислим предел отношения (1.1) при стремлении 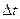к нулю:

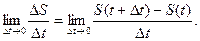
Предел отношения этих величин, если он существует и конечен, и принимается за мгновенную (истинную) скорость движения тела в момент времени 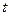(в точке ):

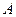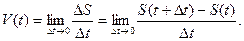(1.2)

В математическом анализе предел (1.2) называется производной функции 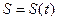по независимой переменной 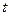и обозначается символом :

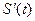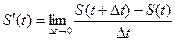. (1.2^*)

Таким образом, мгновенная скорость движения тела – это производная пути по времени:

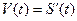(1.3)

Дадим общее определение производной.

Пусть функция 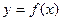определена в интервале 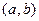. Придадим значению аргумента 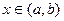произвольное приращение (положительное или отрицательное) 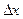, такое, чтобы число 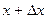не выходило за пределы 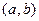. Тогда функция 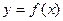получит приращение .

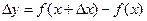Определение.1.1. Производной функции 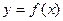в точке называется предел отношения приращения функции 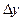к вызвавшему это приращение приращению аргумента 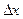, когда 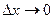(если этот предел существует) и обозначается символом:

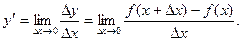(1.4)

Вот наиболее употребительные обозначения производной:

.

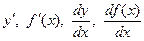Заметим, что процесс нахождения производной носит еще и название дифференцирования функции. O функции, имеющей производную, говорят: функция дифференцируема.

Формула (1.3) выражает механический смысл производной: Производная пути по времени – это скорость движения тела в данный момент времени.

Большое значение в теоретических исследованиях и практических приложениях имеет геометрическое представление производной функции. Выяснением геометрического смысла производной функции мы и займемся.

Дата добавления: 2014-01-07