
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 2. Множество вещественных чисел (продолжение)
|
|
|
|
П.1 Понятия  и
и 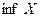
ОПР. Числовое множество Х называют ограниченным сверху, если найдется число М, для которого 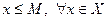 .
.
ОПР. Числовое множество Х называют ограниченным снизу, если найдется число m, для которого  .
.
ОПР. Числовое множество Х называют ограниченным, если найдутся числа m и М, для которых  .
.
Наименьшее из чисел М, ограничивающих сверху множество Х, называют точной верхней гранью этого множества. Аналогично, наибольшее из чисел m, ограничивающих множество Х снизу, называют точной нижней гранью множества Х. Точнее об этом в
ОПР. Число  называют точной верхней гранью множества Х,
называют точной верхней гранью множества Х, , если выполнены два условия:
, если выполнены два условия:
1) 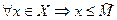 , 2)
, 2)  .
.
ОПР. Число 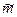 называют точной нижней гранью множества Х,
называют точной нижней гранью множества Х,  , если выполнены два условия
, если выполнены два условия
1) 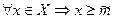 ,2)
,2) 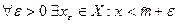 .
.
Точные верхняя и нижняя грани множества Х могут не принадлежать множеству Х.
ПРИМЕР 1. Множество Х является множеством значений последовательности  . Найти
. Найти  и
и 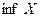 .
.
РЕШЕНИЕ. Докажем, что 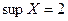 . Действительно,
. Действительно, 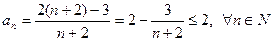 . Для любого
. Для любого 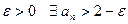 . Решаем последнее неравенство относительно n:
. Решаем последнее неравенство относительно n:  . Заметим, что
. Заметим, что  . Поскольку последовательность
. Поскольку последовательность 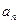 возрастающая, то
возрастающая, то
 , т.е.
, т.е.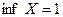 и
и  .
.
ТЕОРЕМА 1. Любое непустое, ограниченное сверху множество  , имеет
, имеет  .
.
ДОК. Пусть У – множество верхних граней множества Х: 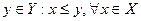 . По аксиоме о полноте множества вещественных чисел (аксиома 5), найдется число
. По аксиоме о полноте множества вещественных чисел (аксиома 5), найдется число  , для которого
, для которого
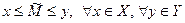 .
.
Таким образом,  и является в нем наименьшим элементом, т.е.
и является в нем наименьшим элементом, т.е.  .
.
Замечание. Множество Х имеет только одну точную верхнюю грань.
ДОК. Пусть  и
и 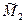 - две такие грани и
- две такие грани и  . Тогда по определению
. Тогда по определению  для
для  найдется
найдется 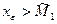 , что противоречит условию
, что противоречит условию  .Аналогично доказывается
.Аналогично доказывается
ТЕОРЕМА 2. Любое непустое, ограниченное снизу множество  , имеет и единственное
, имеет и единственное 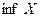 .
.
П.2 Множество рациональных чисел Q.
Числа вида 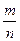 ,
, 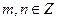 ,
, 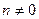 называются рациональными. Два рациональных числа
называются рациональными. Два рациональных числа 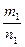 и
и  равны, если
равны, если  .
.
Множество  называется всюду плотным в
называется всюду плотным в 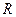 , если
, если 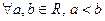
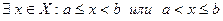 .
.
ТЕОРЕМА 3. Множество Q рациональных чисел всюду плотно в R.
ДОК. Пусть 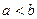 два произвольных вещественных числа. Выберем натуральное n, для которого
два произвольных вещественных числа. Выберем натуральное n, для которого 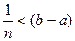 . Пусть К множество целых чисел
. Пусть К множество целых чисел 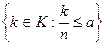 . Множество К ограничено сверху и существует
. Множество К ограничено сверху и существует 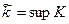 , притом
, притом 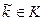 . Тогда
. Тогда  .
.
ОПР. Два множества Х и У называются равномощными, если существует биекция 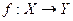 .
.
ОПР. Множество Х равномощное с N называется счетным.
ТЕОРЕМА 4. Множество Q счетно.
ДОК. Покажем, что всякое бесконечное подмножество У счетного множества Х также счетно.  .
.
Тогда 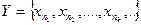 и отображение
и отображение 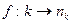 является биекцией
является биекцией 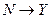 .
.
Рассмотрим множество Х точек на плоскости с координатами 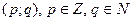 . Множество Х счетно.
. Множество Х счетно.
(соответствующая биекция изображена на рис.) 
Рассмотрим подмножество  , состоящее из пар
, состоящее из пар 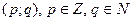 , для которых дробь
, для которых дробь 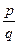 несократима.
несократима.
По доказанному, множество  счетно и отображение
счетно и отображение  биективно. Тогда отображение
биективно. Тогда отображение 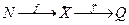 биекция и множество рациональных чисел счетно.
биекция и множество рациональных чисел счетно.
П.3 Система вложенных отрезков.
ОПР. Система отрезков  называется системой вложенных отрезков, если
называется системой вложенных отрезков, если  .
.
ТЕОРЕМА 5. Любая система вложенных отрезков имеет общую точку.
ДОК. Рассмотрим множества 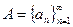 и
и  . Множества А и В ограничены и
. Множества А и В ограничены и  . Тогда по аксиоме полноты существует
. Тогда по аксиоме полноты существует 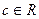 , для которого
, для которого
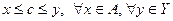 ., т.е
., т.е 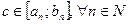 .
.
ОПР. Система вложенных отрезков называется стягивающейся, если  .
.
ТЕОРЕМА 6. Система стягивающихся отрезков имеет единственную общую точку.
ДОК. Пусть с1 и с2 две такие точки и
 .
.
Тогда 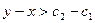 ,т.е.
,т.е. .
.
Последнее противоречит условию стягивания.
ТЕОРЕМА 7. Множество всех точек отрезка  несчетно.
несчетно.
ДОК. Предположим обратное:  . Разобьем отрезок
. Разобьем отрезок  и выберем тот из отрезков, который не содержит х1. Далее полученный отрезок разобьем на три части и выберем тот, который не содержит х2 и т.д. Полученная совокупность вложенных отрезков стягивающаяся. По теореме 1 существует число
и выберем тот из отрезков, который не содержит х1. Далее полученный отрезок разобьем на три части и выберем тот, который не содержит х2 и т.д. Полученная совокупность вложенных отрезков стягивающаяся. По теореме 1 существует число  , не совпадающее ни с одним из xn. Полученное противоречие доказывает, что множество [0;1] несчетно. Множества равномощные с [0;1] называются множествами мощности континуума.
, не совпадающее ни с одним из xn. Полученное противоречие доказывает, что множество [0;1] несчетно. Множества равномощные с [0;1] называются множествами мощности континуума.
УПРАЖНЕНИЯ.
1. Докажите, что множество всех интервалов (а;в) с рациональными концами счетно.
2. Докажите, что множество попарно не пересекающихся интервалов на действительной оси, конечно или счетно.
3. Множество всех последовательностей, состоящих из нулей и единиц, имеет мощность континуума.
ВОПРОСЫ к ЭКЗАМЕНУ.
1) Числовые множества. Понятие точной верхней и нижней грани. Теорема о существовании точной верхней и нижней грани ограниченного числового множества.
2) Множество рациональных чисел. Теорема о всюду плотности рациональных чисел.
3) Счетные множества. Теорема о счетности множества рациональных чисел.
4) Система вложенных отрезков. Теорема о непустоте их пересечения. Система стягивающихся вложенных отрезков. Теорема об единственности точки их пересечения.
5) Теорема о несчетности множества точек отрезка вещественной оси.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 666; Нарушение авторских прав?; Мы поможем в написании вашей работы!