
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 6. Предел функции 2
|
|
|
|
П1. ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
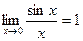 .
.
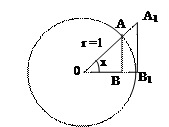
ДОК. (см. рис) Для всех 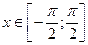 справедливы неравенства:
справедливы неравенства: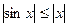 (
(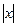 - длина дуги АВ1, а
- длина дуги АВ1, а  - длина дуги катета АВ) и
- длина дуги катета АВ) и 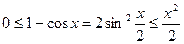 .
.
 Функция
Функция 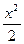 б.м.ф. в точке
б.м.ф. в точке 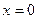 и поэтому, на основании теоремы о промежуточной функции,
и поэтому, на основании теоремы о промежуточной функции, 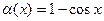 также б.м.ф.Тогда из теоремы о связи
также б.м.ф.Тогда из теоремы о связи 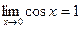 .
.
Площадь D ОАВ 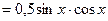 , площадь сектора АОВ1
, площадь сектора АОВ1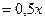 , площадь DОА1В1
, площадь DОА1В1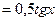 .Справедливо неравенство: площадь D ОАВ< площадь сектора ОАВ< площадь DОА1В1
.Справедливо неравенство: площадь D ОАВ< площадь сектора ОАВ< площадь DОА1В1
Þ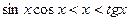 Þ
Þ .
.
По доказанному 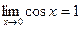 , поэтому на основании теорем о промежуточной функции и арифметической теореме о пределах
, поэтому на основании теорем о промежуточной функции и арифметической теореме о пределах 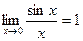 .
.
ПРИМЕР. Вычислить  .
.
РЕШЕНИЕ. 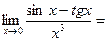
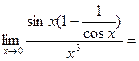
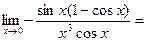
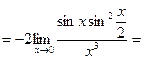
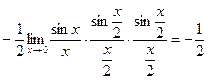 .
.
П.2 ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ.
 .
.
ДОК. (1) Пусть 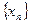 произвольная последовательность,
произвольная последовательность, 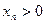 ,для которой
,для которой 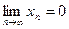 .
.
Тогда 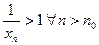 и для каждого n найдутся натуральные числа
и для каждого n найдутся натуральные числа 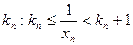 или
или 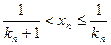 . Справедливо неравенство
. Справедливо неравенство
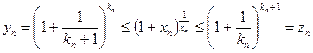 .
.
Последовательности 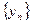 и
и  сходятся к числу e, поэтому на основании теоремы о промежуточной последовательности
сходятся к числу e, поэтому на основании теоремы о промежуточной последовательности  по Гейне, а значит и по Коши.
по Гейне, а значит и по Коши.
(2) Пусть 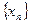 - произвольная последовательность,
- произвольная последовательность, 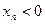 , для которой
, для которой 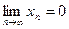 .Обозначим
.Обозначим 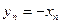 . Тогда
. Тогда
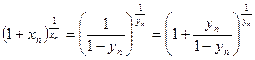 .
.
Обозначим  .Тогда
.Тогда 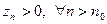 и
и 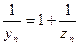 . Из доказанного в (1) следует, что
. Из доказанного в (1) следует, что 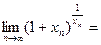

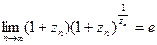 .
.
СЛЕДСТВИЯ (1) 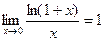 .
.
ДОК. 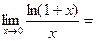
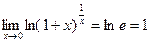
(2)  .
.
ДОК. Замена 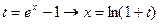 .
.
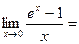
 .
.
П 3. Сравнение функций.
ОПР. (О – большое) Рассматриваются функции 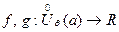 . Говорят, что функция
. Говорят, что функция 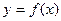 есть
есть
О-большое от функции 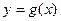 в окрестности точки
в окрестности точки 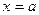 ,
,
обозначение 
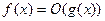 , если
, если
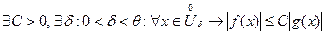 .
.
ПРИМЕР. 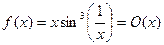 в окрестности точки
в окрестности точки 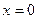 . РЕШЕНИЕ.
. РЕШЕНИЕ. 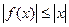 .
.
Если 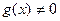 в окрестности
в окрестности 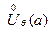 , то условие
, то условие 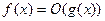 равносильно ограниченности функции
равносильно ограниченности функции 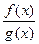 в окрестности точки
в окрестности точки 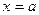 . Последнее выполняется, например, если существует
. Последнее выполняется, например, если существует  .
.
ОПР. (о – маленькое)
Функция 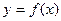 есть о-малое от функции
есть о-малое от функции 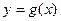 в окрестности точки
в окрестности точки 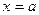 , обозначение
, обозначение 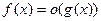 , если
, если 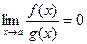 .
.
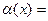 о(1) – бесконечно малая функция Û
о(1) – бесконечно малая функция Û 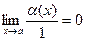 .
.
ПРИМЕР. Алгебра о- малых.(в точке x = 0)
(1) 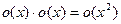 (2)
(2) 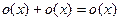 (3)
(3) 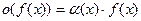 , где
, где 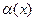 - б.м.ф. (4)
- б.м.ф. (4) 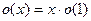
РЕШЕНИЕ. (1) 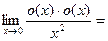
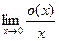
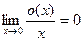
(2) 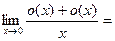

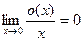 .
.
(3)  Þ
Þ 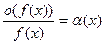 , б.м.ф.
, б.м.ф.
(4) 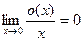 Þ
Þ 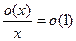 Þ
Þ 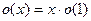 .
.
ОПР. Бесконечно малые в точке 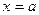 функции
функции 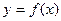 и
и 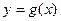 называются эквивалентными, если
называются эквивалентными, если 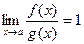 .
.
Обозначение 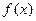 ~
~ 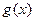 . Отношение эквивалентности транзитивно:
. Отношение эквивалентности транзитивно: 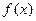 ~
~ 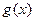 ,
, 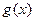 ~
~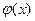 , то
, то 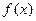 ~
~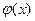 и симметрично:
и симметрично: 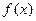 ~
~ 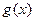 ®
® 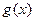 ~
~ 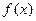 .
.
ТАБЛИЦА ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ в точке x = 0.
(1) 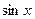 ~
~ 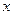
(2) 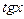 ~
~ 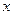 , (3)
, (3)  ~
~ 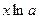 , 4)
, 4) 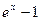 ~
~ 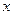 ,
,
(5) 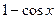 ~
~ 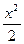 , 6)
, 6) 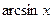 ~
~ 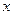 , (7)
, (7)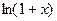 ~
~ 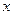 ,
,
(7) 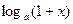 ~
~  ,(8)
,(8) 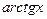 ~
~ 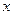 , (9)
, (9)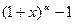 ~
~ 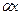
ДОК. Формулы (1)- (3), (6), (8) уже обсуждались, (7) и (9) получаются из них переходом к основанию e, сделав замену 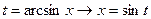 и
и 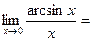
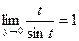 , (5) – аналогично, (10)
, (5) – аналогично, (10) 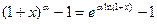 ~
~ 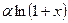 ~
~ 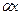 .
.
ТЕОРЕМА 1 (о замене бесконечно малой на эквивалентную)
Если бесконечно малые функции 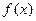 ~
~ 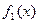 ,
, 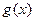 ~
~  в точке
в точке 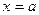 , и существует
, и существует 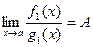 , то
, то 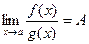 .
.
ДОК. 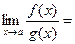
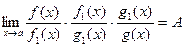 .
.
ТЕОРЕМА 2. (о связи эквивалентных бесконечно малых)
Если две бесконечно малые функции 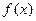 и
и 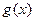 эквивалентны в точке
эквивалентны в точке 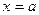 , то
, то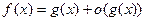 . Если бесконечно малые функции
. Если бесконечно малые функции 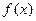 и
и 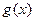 связаны соотношением
связаны соотношением
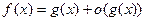 ,то они эквивалентны.
,то они эквивалентны.
ДОК.(1) 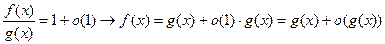
(2)
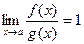 .
.
П 4. Пределы на бесконечности. Односторонние пределы.
ОПР. Функция 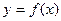 имеет предел на бесконечности, обозначение
имеет предел на бесконечности, обозначение 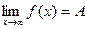 , если
, если
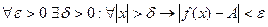 .
.
ОПР. Функция 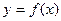 имеет предел в точке
имеет предел в точке 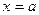 справа, обозначение
справа, обозначение 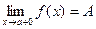 , если
, если
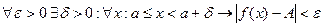 .
.
ОПР. Функция 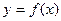 имеет предел в точке
имеет предел в точке 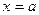 слева, обозначение
слева, обозначение  , если
, если 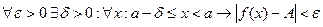 .
.
ОПР. Функция 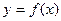 имеет предел на
имеет предел на 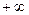 , обозначение
, обозначение 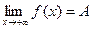 , если
, если  .
.
ОПР. Функция 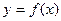 имеет предел на
имеет предел на 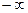 , обозначение
, обозначение 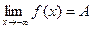 , если
, если 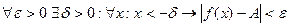 .
.
УПРАЖНЕНИЯ 1) Сформулируйте понятие 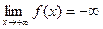 .
.
2) Сформулируйте понятие 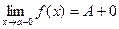 .
.
ВОПРОСЫ К ЭКЗАМЕНУ.
1) Первый замечательный предел.
2) Второй замечательный предел и его следствия.
3) Понятия  и
и 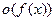 . Примеры.
. Примеры.
4) Эквивалентные бесконечно малые функции, таблица эквивалентных бесконечно малых функций (с доказательством).
5) Теорема о замене бесконечно малой на эквивалентную.
6) Теорема о связи эквивалентных бесконечно малых функций.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 326; Нарушение авторских прав?; Мы поможем в написании вашей работы!