Формализация задачи оптимизации САР

В инженерной практике при разработке систем управления для промышленных объектов задачу синтеза системы автоматического регулирования (САР) подвергают декомпозиции, т.е. её подразделяют на две взаимосвязанные задачи: 1) структурный синтез устройства управления (УУ); 2) оптимальный параметрический синтез (ОПС) УУ.

Для постановки задачи ОПС необходимо иметь:

1) математическую модель объекта регулирования (W^o);

2) математические модели входных воздействий (F, Y^зд);

3) математическую модель эффективности управления I (критерий оптимальности);

4) ограничения на структуру УУ (R_j^доп);

5) ограничения на параметры УУ ().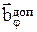

Будем считать, что алгоритм управления j^* (структура УУ), удовлетворяющий условию j^*ÎR_j^доп, успешно определён. Тогда задача оптимального параметрического синтеза САР может быть сформулирована так: необходимо найти такие значения параметров УУ 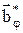, удовлетворяющие ограничениям 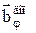, чтобы при заданных моделях объекта регулирования W^o и входных воздействий F, Y^зд выбранный критерий оптимальности I достигал бы своего наилучшего (экстремального) значения

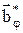=argmin(max) I(W^o, F, Y^зд, j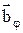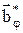^*,,Î).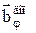

Процедуру ОПС можно отразить в виде следующей схемы (см. рис. 3.15).

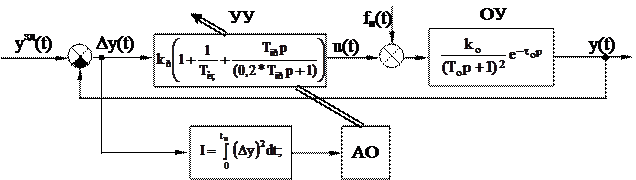
Рис. 3.15

В ходе параметрической оптимизации значения настроечных параметров УУ системы, соответствующие экстремуму критерия оптимальности, определяются путём их целенаправленного перебора. Стратегия перебора задаётся алгоритмом оптимизации (АО). При этом важно, чтобы критерий оптимизации I имел экстремум в пространстве оптимизируемых параметров.

Оптимизация как процедура моделирования реализуется программным пакетом “Блок ОПС САР и её грубость” с использованием инженерной системы MatLab. “Блок ОПС САР и её грубость” обеспечивает выполнение алгоритма оптимизации, который базируется на методе Нелдера-Мида.

Структурная схема процедуры моделирования представлена на рис. 3.16.

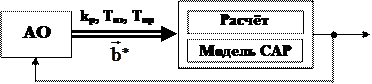Рис. 3.16

Дата добавления: 2014-01-07