Биномиальное распределение

Говорят, что дискретная случайная величина Х имеет биномиальное распределение, если её возмож­ные значения: 0,1, …, m, …, n, а соответствующие вероятности:

P_m=P{X=m}=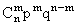, (5.1.1)

где 0<p<1; q=1-p; m=0,1,…,n.

Распределение (5.1.1) зависит от двух параметров n и р.

На практике биномиальное распределение возникает при следующих условиях. Пусть производится n независимых опытов (напомним, что опыты называются независимыми, если вероятность какого-либо исхода каж­дого из них не зависит от того, какие исходы имели другие опыты), в каждом из которых событие А (условно можно его назвать «успехом» опыта) появляется с вероятностью р; случайная величина Х – число «успехов» при n опытах.

Покажем, что случайная величина Х имеет биномиальное распределение. Действительно, событие В={X= m } распадается на ряд вариантов, в каждом из которых «успех» достигается в m опытах, а «неус­пех» (событие 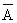) в n-m опытах. Обозначая «успех» знаком +, а «неуспех» знаком -, запишем один из таких вариантов:

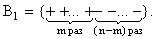
По правилу умножения вероятностей P(B₁)=p^m(1-p)^n-m или, обозначая q=1-p, P(B₁)=p^mq^n-m.

Очевидно, точно такую же вероятность будет иметь любой вариант, в котором m «успехов» и (n-m) «неуспехов»

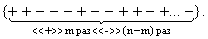
Подсчитаем число таких вариантов. Оно равно 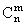, т.е. числу способов, какими можно из n опытов выбрать m «успешных». Отсюда, по правилу сложения вероятностей, складывая вероятности всех 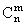вариантов со­бытия B={X= m }, получим

P_m=P{X=m}=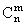pⁿq^n-m,

т.е. случайная величина Х имеет биномиальное распределение. В частности,

P₀=P{X=0}=P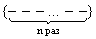=qⁿ,

что также вытекает из формулы (5.1.1), учитывая, что 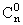==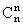1.

Равным образом формула (5.1.1) справедлива и для m=n: .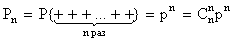

На практике часто приходится вычислять вероятности «не менее m успехов в n опытах»; будем их обозначать R_m:

R_m=P{X³m}=P{X=m}+P{X=m+1}+…+P(X=n}

или 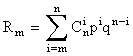. (5.1.2)

Иногда бывает удобнее вычислять R_m через вероятность противоположного события:

R_m= P{X³m}=1-P{X<m},

т.е. 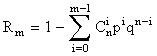. (5.1.3)

Какой из формул (5.1.2), (5.1.3) пользоваться, зависит от того, в какой из них сумма содержит меньше членов.

Найдем важнейшие числовые характеристики случайной величины Х, распределенной по биноми­альному закону. Для этого напишем её производящую функцию:

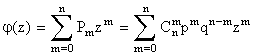; (5.1.4)

но мы знаем, что именно так выглядит n -я степень бинома

j(z)=(q+pz)ⁿ (5.1.5)

(отсюда и термин «биномиальное распределение»).

Пользуясь производящей функцией, найдем числовые характеристики случайной величины Х: мате­матическое ожидание и дисперсию. Дифференцируя (5.1.5) по z, имеем:

j’(z)=n(q+pz)^n-1p.

Полагая здесь z=1, получим

j’(1)= n(q+p)^n-1p= n×1^n-1×p=np.

Итак, математическое ожидание случайной величины Х, распределенной по биномиальному закону с параметрами n и p, равно

m_x=np. (5.1.6)

Заметим, что получить этот результат непосредственно из ряда распределения без производящей функции было бы несравненно труднее.

Аналогично находим второй начальный момент по формуле (2.37) (a₂[X]=a₂=j¢¢(1)+j¢(1)):

a₂=j”(1)+m_x.

Имеем j”(z)=n(n-1)(q+pz)^n-2p²; j”(1)=n(n-1)p².

Второй начальный момент

a₂=j”(1)+m_x=n(n-1)p²+np. (5.1.7)

Дисперсию случайной величины Х найдем, вычитая из (5.1.7) :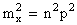

D_x=n(n-1)p²+np-n²p²=n²p²-np²+np-n²p²=np-np²=npq.

Таким образом, дисперсия случайной величины Х, имеющей биномиальное распределение с пара­метрами n, p, равна

D_x=npq (q=1-p). (5.1.8)

Извлекая, квадратный корень из дисперсии, получим среднее квадратическое отклонение:

s_x=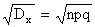. (5.1.9)

Итак, для случайной величины Х, распределенной по биномиальному закону с параметрами n, p,

m_x=np, D_x=npq, . (5.1.10)

Эти выражения полезно запомнить.

Пример 1. Передается n=5 сообщений по каналу связи. Каждое сообщение с вероятностью р =0,3 не­зависимо от других искажается. Случайная величина Х – число искаженных сообщений. Построить её ряд распределения. Найти её математическое ожидание, дисперсию и среднее квадратическое отклоне­ние непосредственно по ряду распределения и сравнить с теми, которые дают формулы (5.1.10). Найти вероятность того, что будет искажено не менее двух сообщений.

Решение. Случайная величина Х – число искаженных сообщений – распределена по биномиальному закону (под «опытом» разумеется передача сообщения, а под «успехом» - его искажение).

По формуле (5.1.1) находим:

P₀=q⁵=0,7⁵=0,16807; P₁=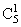×p×q⁴=5×0,3×0,7⁴=0,36015; P₂=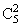p²q³=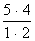×0,3²×0,7³=0,30870;

P₃=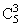p³q²=0,13230; P₄=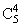p⁴q=0,02835; P₅=p⁵=0,00243.

Или, приближенно, с точностью до 0,001:

Р₀=0,168; Р₁=0,360; Р₂=0,309; Р₃=0,133; Р₄=0,028; Р₅=0,002

(значение Р₃ округлено в большую сторону, чтобы сумма всех вероятностей P_m была не 0,999, а ровно 1).

Приближенно ряд распределения будет иметь вид: .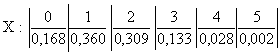

Пользуясь приближенным рядом распределения, находим математическое ожидание случайной ве­личины Х:

m_x=0×0,168+1×0,360+2×0,309+3×0,133+4×0,028+5×0,002=1,499.

Первая из формул (5.1.10) дает для m_x более точное значение: m_x=5×0,3=1,5.

Имея в виду возможность ошибок, хоть и незначительных, дисперсию D_x вычисляем, пользуясь не приближенными, а точными значениями Р_m. Второй начальный момент

a₂=0²×0,16807+1²×0,36015+2²×0,30870+3²×0,13230+4²×0,02835+5²×0,00243=3,30.

Вычитая из a₂ точное значение 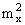=2,25, получим D_x=1,05, что совпадает с результатом, даваемым второй формулой (5.1.10). Среднее квадратическое отклонение равно

.

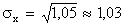Найдем вероятность R₂ того, что будет искажено не менее двух сообщений:

R₂=P{X³2}=1-P{X<2}=1-(P₀+P₁)»0,472.

Пример 2. Игральная кость бросается четыре раза. Найти вероятности того, что шестерка появится а) ровно один раз; б) хотя бы один раз.

Решение: случайная величина Х – число появлений шестерки – имеет биномиальное распределение с параметрами n =4; p =1/6.

a) P{X=1}=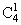p(1-p)³=4(1/6)(5/6)³»0,386.

б) Вероятность R₁=P{X³1}=1-P{X<1}=1-P₀=1-(5/6)⁴=1-0,483=0,517.

В ряде задач практики приходится иметь дело не с биномиальным распределением, а с его обобще­нием на случай, когда вероятность «успеха» в n независимых опытах не постоянна, а меняется от опыта к опыту: в i -ом опыте она равна p _i (i =1,2,…, n). Будем называть это распределение обобщенным биноми­альным.

Производящая функция случайной величины Х, распределенной по обобщенному биномиальному закону, имеет вид:

j(z)=(q₁+p₁z) (q₂+p₂z)… (q_n+p_nz) (5.1.11)

или, короче,

j(z)=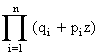, (5.1.12)

где q _i=1- p _i.

Нетрудно убедиться, что, перемножая биномы (5.1.12) и приводя подобные члены с одинаковыми степенями z, мы получим

j(z)=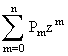, (5.1.13)

где P_m – сумма всех возможных произведений, в которые входят m букв p _i с разными индексами и (n-m) букв q _i c разными индексами. Но точно по такому же алгоритму составляются и коэффициенты при z^m в разложении производящей функции (5.1.12) по степеням z.

При вычислении вероятностей P_m в обобщенном биномиальном распределении часто бывает удобнее не перебирать все возможные комбинации распределений, а перемножать биномы производящей функ­ции.

Важнейшие числовые характеристики случайной величины Х, имеющей обобщенное биномиальное распределение, равны:

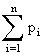m_x=; D_x=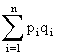. (5.1.14)

Формулы (5.1.14) можно было бы вывести, исходя из производящей функции (5.1.12), но их можно получить гораздо более простым путем, используя теоремы о числовых характеристиках, которые, однако, не входят в наш курс.

Пример 3. По каналу связи передаются четыре сообщения. Каждое из них, независимо от других, может быть искажено. Первое сообщение искажается с вероятностью р ₁=0,1, второе – с вероятностью р ₂=0,2, третье – с вероятностью р ₃=0,3, четвертое – с вероятностью р ₄=0,4, случайная величина Х – число искаженных сообщений. Пользуясь производящей функцией, построить ряд распределения слу­чайной величины Х. Найти вероятность того, что будет искажено: а) хотя бы одно сообщение, б) не ме­нее двух сообщений. Найти – непосредственно и по формулам (5.1.14) – её числовые характеристики: m_x, D_x и s_х.

Решение. Производящая функция:

j(z)=(q₁+p₁z)(q₂+p₂z)(q₃+p₃z)(q₄+p₄z)=(0,9+0,1z)(0,8+0,2z)(0,7+0,3z)(0,6+0,4z)= =0,3024+0,4404z+0,2144z²+0,0404z³+0,0024z⁴.

Ряд распределения случайной величины Х имеет вид:

;

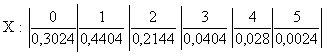m_x=0×0,3024+1×0,4404+2×0,02144+3×0,0404+4×0,0024=1,000.

Тот же результат даст первая формула (5.1.14): m_x=0,1+0,2+0,3+0,4=1.

Дисперсию вычислим не через второй центральный момент, а непосредственно:

D_x=(0-1)²×0,3024+(1-1)²×0,4404+(2-1)²×0,2144+(3-1)²×0,0404+(4-1)²×0,0024=0,7.

Тот же результат получим по второй формуле (5.1.14):

D_x=0,9×0,1+0,8×0,2+0,7×0,3+0,6×0,4=0,7.

Извлекая корень из D_x, получим

.

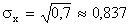Вероятность того, что будет искажено хотя бы одно сообщение и не менее двух сообщений:

R₁=1-P₀=0,6976; R₂=1-(P₀+P₁)=0,2572.

Дата добавления: 2014-01-07