Определение надежности системы по надежности ее элементов. Надежность нерезервированной системы

Надёжность систем

Пусть некоторая техническая система S составлена из n элементов (узлов): Э₁, Э₂, … Э _n.

Допустим, что надежности элементов нам известны. Возникает вопрос об определении надежности системы. Она зависит от того, каким образом элементы объединены в систему, какова функция каждого из них и в какой мере исправная работа каждого элемента необходима для работы системы в целом.

В ряде систем недостаточная надежность элементов повышается за счет их дублирования (резервирования). Резервирование состоит в том, что наряду с элементом Э _i в систему вводится запасной (резервный) элемент Э _i ^’, на который система переключается в случае отказа основного элемента. Число резервных элементов может быть и более одного.

Самым простым случаем в расчетном смысле является простая система (или система без резервирования). В такой системе отказ любого элемента равносилен отказу системы в целом. По аналогии с цепочкой последовательно соединенных проводников, обрыв каждого из которых равносилен размыканию всей цепи, мы будем называть такое соединение «последовательным» (рис. 8.1.1). Следует оговориться, что «последовательным» такое соединение элементов является только в смысле надежности, физически же они могут быть соединены как угодно.

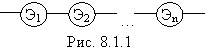
Выразим надежность простой системы через надежность ее элементов. Пусть имеется некоторый промежуток времени (0, t), в течение которого требуется обеспечить безотказную работу системы. Тогда, если надежность системы характеризуется законом надежности P(t), нам важно знать значение этой надежности при t =t, т.е. P(t). Это не функция, а определенное число; отбросим аргумент t и обозначим надежность системы просто P. Аналогично обозначим надежности отдельных элементов p ₁, p ₂, …, p_n.

Для безотказной работы простой системы в течение времени t нужно, чтобы работал безотказно каждый из ее элементов. Обозначим: S – событие, состоящее в безотказной работе системы за время t; Э₁, Э₂, ….Э _n – события, состоящие в безотказной работе соответствующих элементов. Событие S есть произведение (совмещение) событий Э₁, Э₂, ….Э _n:

S = Э₁×Э₂× …×Э _n.

Предположим, что элементы Э₁, Э₂, ….Э _n отказывают независимо друг от друга (или, как мы будем говорить для краткости, «независимы по отказам», а совсем кратко «независимы»). Тогда, по правилу умножения вероятностей для независимых событий

P(S)=P(Э₁)P(Э₂)…P(Э_n),

или в других обозначениях,

Р = р₁×р₂×…×р_n, (8.1.1)

а короче , (8.1.2)

т.е. надежность простой системы, составленной из независимых элементов, равна произведению надежности ее элементов.

В частном случае, когда все элементы обладают одинаковой надежностью

р₁ =р₂ = … = р_n = р,

формула (8.1.2) принимает вид:

Р=рⁿ. (8.1.3)

Пример 1. Простая система состоит из 10 независимых элементов, надежность каждого из которых равна р=0,95. Определить надежность системы.

Решение. По формуле (8.1.3) Р=0,95¹⁰»0,6.►

Из примера видно, как резко падает надежность простой системы при увеличении числа элементов. Если число элементов n велико, то для обеспечения хотя бы приемлемой надежности Р системы каждый элемент должен обладать очень высокой надежностью.

Поставим вопрос: какой надежность р должен обладать отдельный элемент для того, чтобы система, составленная из n таких элементов, обладала заданной надежностью R?

Полагая в формуле (8.1.3) Р=R, получим:

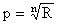. (8.1.4)

Пример 2. Простая система состоит из 1000 одинаково надежных, независимых элементов. Какой надежностью должен обладать каждый из них для того, чтобы надежность системы была не меньше 0,9?

Решение. По формуле (8.1.4): ; 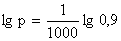, р»0,9999.►

Выразим интенсивность отказов простой системы L(t) через интенсивности отказов l _i (t) отдельных её элементов. Имеем:

,

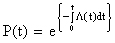, где (i = 1, …, n)

Подставим эти выражения в формулу (8.1.2); получим:

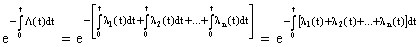
или, короче ,

откуда . (8.1.5)

Дифференцируя (8.1.5) по t, получим:

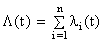, (8.1.6)

т.е. при «последовательном» соединении независимых элементов интенсивности отказов складываются.

Это и естественно, так как для простой системы отказ элемента равносилен отказу системы, значит, все потоки отказов отдельных элементов складываются в один поток отказов системы с интенсивностью, равной сумме интенсивностей отдельных потоков.

Пример 3. Простая система S состоит из трех независимых элементов Э₁, Э₂, Э₃(рис.8.1.2),

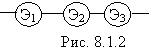
плотности распределения времени безотказной работы которых заданы формулами:

,

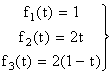при 0 < t <1

(рис. 8.1.3-8.1.5). Найти интенсивность отказов системы.

Решение. Определяем ненадежность каждого элемента:

, при 0 < t <1.

Отсюда надежности элементов

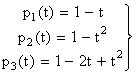, при 0 < t <1.

Интенсивность отказов элементов:

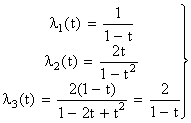, при 0 < t <1.

Складывая, имеем: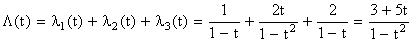

8.2. Надежность резервированной системы («горячий резерв»)

Одним из путей повышения надежности системы является введение в нее дублирующих (резервных элементов). Резервные элементы включаются в систему как бы «параллельно» тем, надежность которых недостаточна.

Рассмотрим самый простой пример резервированной системы: два «параллельно» включенных элемента Э₁ и Э₂ (рис. 8.2.1). Вначале работает основной элемент Э₁; если он отказал, система автоматически переключается на «резервный» элемент Э₂.

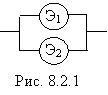
Предположим, что элементы Э₁ и Э₂ независимы по отказам и что их надежности (вероятности безотказной работы) за интересующее нас время t=t равны соответственно р ₁ и р ₂. Предположим также, что надежность второго элемента не зависит от того, включался ли этот элемент в работу за время t и когда включался. Такая картина наблюдается, например, если элемент Э₂ независимо от того, работает он или нет, держится под рабочим напряжением (так называемый «горячий резерв»).

Определим при этих условиях надежность резервированной системы S. Перейдем к вероятности противоположного события – отказа системы S. Обозначим отказ системы . Чтобы событие произошло, необходимо, чтобы отказали оба элемента: и первый и второй: .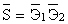

Отсюда по правилу умножения вероятностей независимых событий: .

Обозначая ненадежность системы Q, а ненадежности элементов q₁, q₂, получим:

Q=q₁q₂, (8.2.1)

т.е. при «параллельном» соединении независимых элементов их ненадежности перемножаются.

Переходя в формуле (8.2.1) от ненадежностей к надежностям, имеем:

1 – Р = (1 – р ₁) (1 – р ₂),

откуда Р = 1 – (1 – р ₁) (1 – р ₂). (8.2.2)

При произвольном числе n дублирующих друг друга независимых элементов надежность блока из таких элементов (рис. 8.2.2) вычисляется по формуле

Р = 1 – (1 – р ₁) (1 – р ₂)... (1 – р_n), (8.2.3)

или, короче

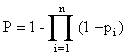. (8.2.4)

В частном случае, когда надежности всех элементов одинаковы: р ₁ = р ₂ = … = р,

формула (8.2.4) принимает вид:

Р = 1 – (1 –р)ⁿ. (8.2.5)

Пример 1. Предохранительное устройство, обеспечивающее безопасность работы с материальной частью, состоит из трех дублирующих друг друга предохранителей. Надежность каждого из них р =0,9. Предохранители независимы в смысле надежности. Найти надежность всего устройства.

Решение. По формуле (8.2.5) Р=1–(1–0,9)³ = 0,999.

До сих пор, говоря о «переключении» на резервный элемент, мы предполагали, что либо для этого не требуется специального переключающего устройства (как в случае с предохранителями), либо надежность переключающего устройства равна единице. Если это не так, то легко учесть его неполную надежность.

Предположим, что блок состоит из двух «параллельно» включенных элементов Э₁ и Э₂ (рис. 8.2.3). В случае, когда элемент Э₁ выходит из строя, переключающее устройство П переключает систему на другой, резервный элемент Э₂. Надежности элементов Э₁, Э₂ и переключателя П равны соответственно р ₁, р ₂ и р _п. Определим надежность всего блока. Для этого объединим переключатель П и элемент Э₂ в одну «последовательную» цепь с надежностью р ₂’ = р _п р ₂.

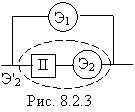
Рассматривая эту цепочку как один параллельно включенный условный элемент Э₂’, найдем по формуле (8.2.2) надежность блока

Р = 1 – (1 – р ₁) (1 – р ₂’) = 1 – (1 – р ₁) (1 – р _п р ₂). (8.2.6)

Таким образом, неполная надежность переключателя может быть учтена простым умножением надежности резервного элемента на надежность переключателя.

Если резервных элементов не один, а больше: Э₂, …, Э _n и каждый из них снабжен своим переключателем с надежностью соответственно 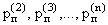, то в формуле (8.2.3) нужно умножить надежность каждого резервного элемента на надежность переключателя:

Р = 1 – (1 – р ₁) (1 – р _П⁽²⁾ р ₂) (1 – р _П⁽³⁾ р ₃) … (1 – р _П⁽ⁿ⁾ (8.2.7)

Может оказаться, что переключение на любой резервный элемент осуществляется одним и тем же переключателем П (рис. 8.2.4). Тогда переключатель П вместе со всем блоком резервных элементов может рассматриваться как один условный элемент Э₂’ с надежностью р ₂’, равной

р ₂’ = р _П [(1 – (1 – р ₂) (1 – р ₃) … (1 – р_n)], (8.2.8)

а надежность всего блока вычислится по формуле

Р = 1 – (1 – р ₁) (1 – р ₂’). (8.2.9)

Пример 2. Определить надежность блока, состоящего из основного элемента Э₁ с надежностью р ₁=0,9 и трех резервных элементов: Э₂, Э₃, Э₄, имеющих ту же надежность: р ₂ = р ₃ = р ₄ = 0,9.

Переключение на резервные элементы в случае отказа любого из элементов осуществляется с помощью одного и того же переключателя, имеющего надежность р _П = 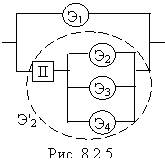0,95 (рис. 8.2.5). Найти надежность блока.

Решение. Объединим переключатель с резервными элементами Э₂, Э₃, Э₄ в условный элемент Э₂’ с надежностью р ₂’ = р _П [1 – (1 – р ₂) (1 – р ₃) (1 – р ₄)] = 0,95 (1 – 0,1³)» 0,949.

Надежность всего блока: Р = 1 – (1 – 0,9) (1 – 0,949)» 0,995.

Заметим, что в данном примере сравнительно низкая надежность переключателя практически обесценивает большое количество (три!) резервных элемента. Значительно большую надежность системы мы получили бы, если бы каждый элемент был снабжен своим переключателем:

Р = 1 – (1 – 0,9) (1 – 0,95 × 0,9)³» 0,9997.

До сих пор мы рассматривали системы, дублирующие один основной элемент. В общем случае в резервированных системах могут применяться как «последовательные», так и «параллельные» соединения элементов, причем как правило, дублируются наименее надежные элементы. При оценке надежности такой системы нужно расчленить ее на ряд «подсистем», не имеющих общих элементов, найти надежность каждой из них и, рассматривая подсистемы как условные элементы, оценить надежность системы в целом.

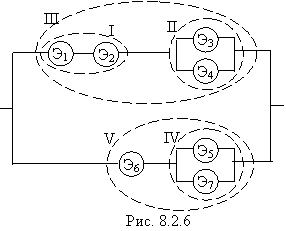
Пример 3. Определить надежность системы, состоящей из элементов Э₁, Э₂, …, Э₇ с надежностями р ₁. р ₂, …, р ₇ (рис. 8.2.6).

Решение. Подсистема I – «последовательно» соединенные элементы Э₁ и Э₂; надежность: Р _I = р ₁ р ₂.

Подсистема II – «параллельно соединенные элементы Э₃ и Э₄; надежность: Р _II = 1 – (1 – р ₃) (1 – р ₄).

Подсистема III – «последовательно» включенные I и II; надежность: Р _III = Р _I Р _II.

Подсистема IV - «параллельно» включенные Э₆ и Э₇; надежность: Р _IV = 1 – (1 – р ₆) (1 – р ₇).

Подсистема V – «последовательно» включенные Э₅ и IV; надежность: Р _V = р ₅ Р _IV.

Вся система – «параллельно» включенные III и V; надежность: Р = 1 – (1 – Р _III) (1 – Р _V).►

Дата добавления: 2014-01-07