Надежность резервированной системы. «Холодный» и «облегченный» резерв

До сих пор мы рассматривали только случай, когда надежность каждого дублирующего элемента не зависит от того, когда включился в работу этот элемент. Этот случай, который мы условно назвали «горячим резервированием», самый простой их всех возможных. Гораздо сложнее случай, когда резервный элемент до своего включения в работу вообще не может отказывать («холодное» резервирование) или может отказывать, но с другой, меньшей плотностью вероятности, чем после включения («облегченное» резервирование).

При рассмотрении задач, связанных с холодным или облегченным резервированием, нам недостаточно будет вводить надежности системы и элементов для одного, заранее фиксированного, значения времени t; необходимо будет проанализировать весь случайный процесс функционирования системы.

Рассмотри несколько задач, относящихся к холодному и облегченному резервированию.

Задача 1. Общий случай расчета надежности резервированной системы («облегченный» или «холодный» резерв). Система (блок) состоит из «параллельно» включенных элементов Э₁ и Э₂ (основного и резервного). Интенсивность потока отказов первого элемента l₁(t); при отказе первого элемента происходит автоматическое и безотказное переключение на резервный (р _П = 1). Интенсивность потока отказов резервного элемента до его включения в работу l₂(t) (элемент работает в «облегченном» режиме). После его включения в работу, в момент отказа первого элемента, интенсивность мгновенно подскакивает (рис.8.3.1) и становится равной интенсивности 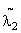, которую естественно предполагать зависящей не только от текущего времени t, но и от того срока t ₁, в течение которого элемент работал в облегченном режиме: .

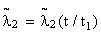Требуется найти надежность системы Р (t).

Рассмотрим совокупность двух случайных величин:

Т ₁ – момент отказа основного элемента,

Т ₂ – момент отказа резервного элемента.

Событие А – безотказная работа системы до момента t – состоит в том, что хотя бы одна из величин Т ₁, Т ₂ примет значение, большее, чем t (хотя бы один элемент будет работать к моменту t). Вероятность противоположного события – отказа системы до момента t будет

Р (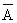) = 1 – Р (А) = Р (Т ₁ < t, T ₂ < t).

Найдем совместную плотность распределения случайных величин Т ₁ и Т ₂, обозначая ее f (t ₁, t ₂). Случайные величины Т ₁, Т ₂ зависимы, и

f (t ₁, t ₂) = f₁ (t ₁) f (t _2½ t ₁). (8.3.1)

где f ₁(t ₁) – безусловная плотность распределения величины Т ₁, f (t _2½ t ₁) – условная плотность распределения величины Т ₂ (при условии, что величина Т ₁ приняла значение t ₁).

Найдем обе плотности. По формуле (3.7) f ₁(t ₁)=l₁(t ₁) р ₁(t ₁),

где р ₁ (t ₁) – надежность элемента Э₁, в силу формулы (3.9) равная .

Отсюда 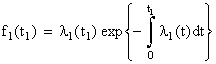. (8.3.2)

Найдем условную плотность ¦(t₂ / t₁). Условная интенсивность отказов резервного элемента при условии, что T₁=t₁, будет:

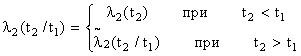(8.3.3)

При этой интенсивности найдем условную плотность распределения времени безотказной работы резервного элемента:

(8.3.4)

Таким образом, совместная плотность распределения системы случайных величин T₁, T₂ найдена: (8.3.5)

Зная эту совместную плотность, можно найти вероятность отказа системы до момента t:

,

откуда искомая надежность системы:

(8.3.6)

При вычислении по формулам (8.3.5) – (8.3.6) необходимо иметь в виду, что выражение функции f(t₁,t₂) неодинаково по одну и другую сторону от прямой t₁= t₂ - биссектрисы первого координатного угла (рис. 8.3.2). Области интегрирования на рис. 8.3.2 отмечены разной штриховкой.

В области I функция f(t₁,t₂)

выражается первой из формул (8.3.5), в области II - второй; следовательно,

. (8.3.7)

При заданном конкретном виде функций l₁(t), l₂(t), l₂(t/t₁) интеграл (8.3.7) может быть вычислен, в простейших случаях аналитически, чаще – численно.

Заметим, что найденное нами решение задачи оценки надежности для случая «облегченного» резерва относится и к случаю «холодного» резерва – при этом l₂(t) =0, так что в формуле (8.3.7) остается только один интеграл – второй, да и тот тоже упростится.

Мы видим, что в случае даже одного резервного элемента, работающего в облегченном (или холодном) резерве задача оценки надежности системы довольно сложна. Если же число резервных элементов более одного, задача еще больше усложняется. В общем виде такие задачи зачастую и не рассматриваются.

Однако задача может быть сильно упрощена, если предположить, что потоки неисправностей, действующие на все элементы (основной и резервный), представляют собой простейшие потоки, интенсивность каждого из которых постоянна (это допущение равносильно тому, что закон надежности каждого элемента – экспоненциальный, а включение элемента в работу меняет только параметр этого закона). При таком допущении надежность системы S может быть найдена путем решения дифференциальных уравнений для вероятностей ее состояний. Для этого метода используются понятия и результаты теории марковских случайных процессов.

Дата добавления: 2014-01-07